Формулы. Обычно понятие центробежной силы используется в рамках классической (Ньютоновской) механики, которой касается основная часть данной статьи (хотя обобщение

Обычно понятие центробежной силы используется в рамках классической (Ньютоновской) механики, которой касается основная часть данной статьи (хотя обобщение этого понятия и может быть в некоторых случаях достаточно легко получено для релятивистской механики).

По определению, центробежной силой называется сила инерции (то есть в общем случае — часть полной силы инерции) в неинерциальной системе отсчета, не зависящая от скорости движения материальной точки в этой системе отсчета, а также не зависящая от ускорений (линейных или угловых) самой этой системы отсчета относительно инерциальной системы отсчета.

Для материальной точки центробежная сила выражается формулой:

где:

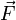— центробежная сила приложенная к телу,

— масса тела,

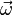— угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика),

— радиус-вектор тела во вращающейся системе координат.

Эквивалентное выражение для центробежной силы можно записать как

если использовать обозначение для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.

Центробежная сила для тел конечных размеров может быть рассчитана (как это обычно делается и для любых других сил) суммированием центробежных сил, действующих на материальные точки, являющиеся элементами, на которые мы мысленно разбиваем конечное тело.

Поиск по сайту: