 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Отношение эквивалентности
Введем очень важный тип бинарных отношений, который можно определить на некотором заданном множестве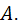 
Опр.1.5.1. Пусть 
. Тогда, если отношение 
1) рефлексивно;
2) симметрично;
3) транзитивно,
то называется отношением эквивалентности.
Примеры отношений эквивалентности: быть параллельными, быть подобными, быть равными.
Общая идея введения отношения эквивалентности – объединить объекты, которые похожи чем-то друг на друга.
Опр.1.5.2. Пусть – отношение эквивалентности, определенное на множестве А. Тогда множество всех элементов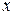 
из 
, таких, что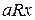 
для некоторого 
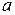называется смежным классом для :
.
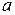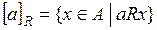Важным является следующее свойство классов смежности.
ТЕОРЕМА 1.5.1. Пусть – отношение эквивалентности на множестве . Тогда оно определяет разбиение , состоящее из смежных классов. Наоборот, всякое разбиение множества задает отношение эквивалентности.
Пример.
Пусть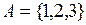 
. Определим отношение эквивалентности 
.
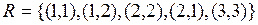Матрица отношения
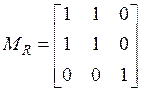
рефлексивна, симметрична, транзитивна (для транзитивных отношений с точностью до ненулевых элементов выполняется соотношение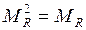 
).
Классы смежности:
.
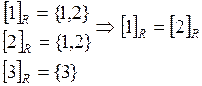Таким образом, разбиение содержит два класса 
. ▲
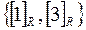Опр. 1.5.3. Совокупность смежных классов множества по эквивалентности называется фактор-множеством по и обозначается как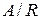 
.
Таким образом, в нашем примере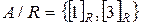 
.
Поиск по сайту: