АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Отношение частичного порядка

Читайте также:
  1. I. IIонятие, виды и соотношение источников МЧП.
  2. IX.6. Взаимоотношение науки и техники
  3. V2: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
  4. А. Базовое системное соотношение.
  5. Апериодическое звено второго порядка.
  6. Б. Наследственное правоотношение
  7. Б. Наследственное правоотношение
  8. Б. Системное соотношение с измененным основным аргументом.
  9. В. Соотношение требований из неосновательного обогащения с другими требованиями о защите гражданских прав
  10. Вещь — свойство — отношение
  11. Вещь, свойство, отношение
  12. Взаимоотношение классов и задачи с.-д. на новом этапе революции

 

Язык теории множеств позволяет довольно просто ввести понятие порядка на множествах любой природы.

 

Опр. 1.6.1. Бинарное отношение 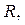определенное на множестве 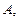которое является

1) рефлексивным;

2) антисимметричным;

3) транзитивным

называется отношением частичного порядка.

 

Примеры отношений частичного порядка:

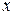, , « делит 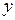на множестве 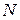». Общее обозначение: .

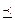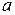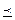
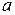Опр. 1.6.2. Пусть – частично-упорядоченное множество. Элемент называется наибольшим в , если x для любого 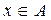, и наименьшим, если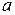 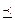x для любого .

 

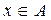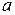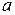Опр.1.6.3. Максимальным элементом частично-упорядоченного множества называется такой его элемент , для которого всякий x из либо не сравним c , либо x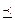 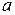(для минимального элемента -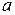 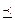x).

Разница между наибольшим и максимальным элементами заключается в том, что наибольший элемент либо отсутствует, либо единственный. Максимальный элемент всегда существует и их может быть несколько. Если наибольший элемент существует, то он автоматически является и максимальным элементом множества с частичным порядком. Аналогично для наименьшего и минимального элементов. Частично упорядоченное множество удобно изображать с помощью диаграмм Хассе, в которых сравнимые элементы, непосредственно следующие друг за другом, изображаются точками, соединенными отрезками.

 

Пример.

Пусть 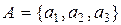. Введем частичный порядок как отношение включения подмножеств: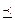 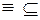, определенном на подмножествах множества 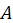, т.е. на булеане .

Диаграмма Хассе будет иметь вид:

 

 

Из диаграммы видно, что

- наибольший элемент ;

- наименьший элемент ;

- подмножества 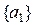и несравнимы. ▲

 

 


1 | 2 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)