 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Принцип соответствия. Релятивистские эффекты
Основы специальной теории относительности (СТО).
Преобразования Лоренца. Принцип относительности Эйнштейна.
Принцип соответствия. Релятивистские эффекты
Развитие учения об электрических и магнитных явлениях, в том числе об электромагнитных волнах, частным случаем которых является свет, поставило ряд вопросов относительно справедливости механистических представлений о пространстве и времени.
Математическим выражением представлений о пространстве и времени в классической механике являются преобразования Галилея (3.5). По механическому принципу относительности законы механики должны быть одинаковыми во всех инерциальных системах отсчета. Если в законах Ньютона и других законах классической механики координаты тел и время в одной системе отсчета заменить на координаты и время в другой инерциальной системе, используя при этом соотношения (3.5), то, как нетрудно показать, вид этих законов совершенно не изменится. Как говорят, законы классической механики оказываются инвариантными (неизменными) относительно преобразований Галилея.
Однако оказалось, что законы электричества и магнетизма относительно преобразований Галилея не инвариантны. Совокупность основных законов электромагнетизма сводится к так называемой системе уравнений Максвелла (вид этих уравнений приводить не будем). Можно показать, что, если верны преобразования (3.5), то вид уравнений Максвелла в разных инерциальных системах различен, то есть электрические и магнитные явления протекают в разных системах по-разному. В частности, скорость распространения электромагнитных волн, то есть скорость света, оказалась бы разной в разных инерциальных системах отсчета и зависела бы от величины и направления скорости движения системы.
Неинвариантность уравнений Максвелла относительно преобразований Галилея означает либо неприменимость принципа относительности к электромагнитным, оптическим и прочим немеханическим явлениям, либо неправильность самих преобразований Галилея.
Ряд тонких экспериментов не смог зафиксировать различий в протекании оптических процессов в разных системах отсчета. Так, А. Майкельсон (амер., Нобелевская премия 1907 г.) в опытах 1886-87 годов попытался заметить изменение скорости света, связанное с орбитальным движением Земли со скоростью 30 км/с, но не обнаружил его.
В 1904 г. Х.А. Лоренц (голл.) математически показал, что система урав-
нений Максвелла будет неизменна во всех инерциальных системах отсчета, если связь координат и времени в таких системах определяется не преобразованиями Галилея (3.5), а следующими преобразованиями, названными впоследствии преобразованиями Лоренца:
где  3·108 м/с - скорость света в вакууме.
3·108 м/с - скорость света в вакууме.
Если верны соотношения (3.7), то электромагнитные и оптические явления протекают одинаково во всех инерциальных системах отсчета, в частности, во всех системах скорость света одинакова. Но в этом случае оказываются неверными представления, сложившиеся в классической механике и в обыденном сознании о свойствах пространства и времени. Например, последнее из уравнений (3.7) означает, что в разных системах отсчета время идет по-разному  . Кроме того, законы Ньютона и другие законы классической механики не инвариантны относительно (3.7). Физического объяснения предложенным преобразованиям Х.А. Лоренц не дал.
. Кроме того, законы Ньютона и другие законы классической механики не инвариантны относительно (3.7). Физического объяснения предложенным преобразованиям Х.А. Лоренц не дал.
Возникшую проблему решил в 1905 г. А. Эйнштейн, создав специальную (частную) теорию относительности (СТО), составной частью которой является релятивистская механика - механика больших, то есть соизмеримых со скоростью света, скоростей. СТО стала первым шагом в современной теории пространства и времени. Вторым шагом является общая теория относительности.
СТО базируется на двух постулатах Эйнштейна, каждый из которых приведем в двух эквивалентных формулировках.
Первый постулат, называемый также принципом относительности Эйнштейна, гласит: никакими опытами (механическими, электрическими, оптическими и прочими), проведенными в замкнутой системе тел, невозможно обнаружить, покоится эта система или движется прямолинейно и равномерно относительно некоторой инерциальной системы отсчета.
Вторая формулировка: все законы природы одинаковы во всех инерциальных системах отсчета.
Второй постулат Эйнштейна, называемый также принципом инвариантности скорости света, гласит: скорость света в вакууме не зависит от скорости движения источника света.
Вторая формулировка: скорость света в вакууме одинакова во всех инерциальных системах отсчета.
Второй постулат фактически утверждает, что в действительности верны преобразования Лоренца (3.7), а не преобразования Галилея (3.5).
Из первого постулата следует, что классическая механика, вообще говоря, неверна и должна быть заменена иной механикой (релятивистской механикой), законы которой инвариантны относительно преобразований (3.7).
Важно, что в случае движения системы  относительно системы
относительно системы  со скоростью
со скоростью 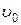 , много меньшей скорости света (
, много меньшей скорости света ( ), преобразования Лоренца сводятся к преобразованиям Галилея, а законы релятивистской механики сводятся к законам механики классической. То есть новая теория (СТО) не отвергла полностью прежнюю (классическую механику), а лишь указала на ограниченность ее применения областью малых скоростей:
), преобразования Лоренца сводятся к преобразованиям Галилея, а законы релятивистской механики сводятся к законам механики классической. То есть новая теория (СТО) не отвергла полностью прежнюю (классическую механику), а лишь указала на ограниченность ее применения областью малых скоростей:
Таким образом, создание теории относительности есть пример развития научного знания согласно важнейшему общенаучному методологическому принципу - принципу соответствия. Этот принцип был выдвинут в 1918 г. Н. Бором (дат.) и устанавливает, что любая новая теория, претендующая на более глубокое описание физической реальности и/или на более широкую область применимости, чем старая, должна включать в себя последнюю как частный предельный случай.
Приведем без доказательства основные результаты СТО.
1. Пусть в инерциальной системе  в точке с координатами
в точке с координатами  в момент
в момент  происходит событие 1, а в точке с координатами
происходит событие 1, а в точке с координатами 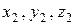 в момент
в момент  происходит событие 2. Разности пространственных и временн ы х координат этих событий в системе
происходит событие 2. Разности пространственных и временн ы х координат этих событий в системе  обозначим так:
обозначим так:  ,
, 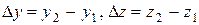 ,
,  . Этим же событиям в другой инерциальной системе отсчета
. Этим же событиям в другой инерциальной системе отсчета  соответствуют координаты и моменты времени
соответствуют координаты и моменты времени  и
и  , и разности
, и разности  .
.
Аксиомы об инвариантности пространственных и временн ы х промежутков, на которых базируется классическая механика, в том числе - преобразования Галилея, математически выражаются следующими равенствами:.
В СТО последние соотношения неверны, то есть пространственные и временн ы е промежутки между двумя событиями различны в разных инерциальных системах отсчета. Но зато инвариантным относительно преобразований Лоренца, то есть одинаковым во всех системах отсчета оказывается так называемый интервал (пространственно-временн о й интервал)  между событиями, квадрат которого есть
между событиями, квадрат которого есть
(3.8)
2. События, одновременные в одной системе отсчета, неодновременны в другой.
3. Длина предмета в направлении движения различна в различных инерциальных системах отсчета: (3.9)
где  - собственная длина, то есть длина предмета в системе, относительно которой предмет покоится (см. рисунок 3.3);
- собственная длина, то есть длина предмета в системе, относительно которой предмет покоится (см. рисунок 3.3); 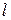 - длина в системе, относительно которой предмет движется.
- длина в системе, относительно которой предмет движется.
Из (3.9) следует, что  ; этот эффект называется релятивистским (лоренцевым) сокращением длины.
; этот эффект называется релятивистским (лоренцевым) сокращением длины.
4. Длительность какого-либо процесса различна в разных системах отсчета: (3.10)
где  - собственная длительность процесса в системе, относительно которой точка протекания процесса неподвижна,
- собственная длительность процесса в системе, относительно которой точка протекания процесса неподвижна,  - длительность процесса в системе, относительно которой точка протекания процесса движется.
- длительность процесса в системе, относительно которой точка протекания процесса движется.
5. Масса тела зависит от скорости его движения:
 (3.11)
(3.11)
где  - масса тела в системе, в которой тело покоится (масса покоя), m - масса движущегося тела (релятивистская масса).
- масса тела в системе, в которой тело покоится (масса покоя), m - масса движущегося тела (релятивистская масса).
6. Тело с ненулевой массой покоя ( ) может двигаться только со скоростью, не превышающей скорость света c.
) может двигаться только со скоростью, не превышающей скорость света c.
7. Со скоростью света могут двигаться только объекты с нулевой массой покоя, например - фотоны.
8. Для расчета движения тел применяется основной закон релятивистской динамики, который по виду совпадает со вторым законом Ньютона классической физики (3.1)  , но в котором зависимость релятивистского импульса
, но в котором зависимость релятивистского импульса  от скорости имеет вид
от скорости имеет вид
 . (3.12)
. (3.12)
9. Энергия тела связана с его релятивистской массой формулой Эйн-
штейна:
 . (3.13)
. (3.13)
10. Если тело покоится и не взаимодействует с другими телами, то есть не имеет ни кинетической, ни потенциальной энергии, то оно, тем не менее, имеет энергию (энергию покоя)  , обусловленную наличием массы покоя:
, обусловленную наличием массы покоя:
 . (3.14)
. (3.14)
11. Поскольку в преобразованиях Лоренца (3.7) в формулу преобразования времени входит координата, то имеет место связь пространства и времени. Нельзя говорить отдельно о пространстве и о времени, а только о едином пространстве-времени, в котором протекают все события.
Для описания физических процессов в СТО используется абстрактное четырехмерное пространство с осями  , в котором для соблюдения единства размерностей по всем осям ось времени заменена осью
, в котором для соблюдения единства размерностей по всем осям ось времени заменена осью 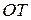 , по которой откладывается величина
, по которой откладывается величина 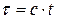 , измеряемая в метрах.
, измеряемая в метрах.
Каждому событию соответствует точка в этом пространстве, движению - линия, называемая мировой линией. Примеры мировых линий для неподвижного тела и фотона представлены на рисунке 3.4., на котором оси 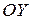 и
и  не показаны ввиду невозможности изобразить на двумерном рисунке четыре взаимно перпендикулярные оси.
не показаны ввиду невозможности изобразить на двумерном рисунке четыре взаимно перпендикулярные оси.
12. Геометрические свойства пространства могут быть определены, если известно, каким образом в данном пространстве определяется расстояние между точками. Для обычного трехмерного пространства, описываемого геометрией Евклида, квадрат расстояния s между точками определяется так:
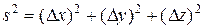 . (3.15)
. (3.15)
Интервал между двумя событиями в четырехмерном пространстве-времени в СТО определяется соотношением (3.8), аналогичным (3.15) за исключением того, что в (3.15) все члены положительны, а в (3.8) временной промежуток входит со знаком плюс, а пространственные со знаком минус. Такое четырехмерное пространство-время, определяемое интервалом вида (3.8), называется псевдоевклидовым или пространством Минковского.
Вообще изучение физических свойств пространства-времени можно свести к чисто геометрическому изучению свойств четырехмерного пространства, если для него известно выражение типа (3.8) или (3.15), определяющее интервал, то есть так называемая метрика. Один из выводов СТО - решение физических проблем может быть сведено к геометрическим исследованиям пространства-времени.
Поиск по сайту: