Приведение уравнения кривой к каноническому виду. Классификация кривых второго порядка на плоскости

Материалы лекции 5

Литература. [1]§ 37, 38.

Рассмотрим кривую g второго порядка. В предыдущем параграфе мы показали, что всегда можно выбрать такую прямоугольную декартовую систему координат, ось ординат которой имеет главное направление относительно этой кривой, в которой уравнение кривой имеет вид:

, (1)

где и ‑ корни характеристического уравнения кривой (характеристические числа кривой). В настоящем параграфе мы проведем полную классификацию кривых второго порядка и рассмотрим примеры нахождения канонического уравнения кривой.

Рассмотрим первый случай, кривая g ‑ центральная, она имеет эллиптический или гиперболический тип, ее первый инвариант отличен от нуля. Из (1) следует, что первый инвариант кривой равен . В этом случае характеристические числа и также отличны от нуля. Без ограничения общности можно считать, что в уравнении (1) коэффициент при положителен, иначе следует поменять знаки у коэффициентов этого уравнения. Выделим полные квадраты в левой части уравнения (1), приведем уравнение к виду: . Осуществим параллельный перенос системы координат по формулам: Введем обозначение . 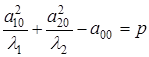Тогда уравнение (21.1) примет вид:

(2)

I. Кривая имеет эллиптический тип. Тогда , . Без ограничения общности можно считать, что и характеристические числа и положительны.

I₁. . Уравнение (21.2) приводится к виду . Если ввести обозначения , то получим: , т.е. каноническое уравнение эллипса. В этом случае кривая представляет собой эллипс. При этом, его центр находится в точке с координатами (проверьте самостоятельно).

I₂. 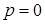. Уравнение (2) можно привести к виду: . Если ввести обозначения: , то окончательно получим: . На плоскости существует только одно точка , координаты которой удовлетворяют этому уравнению. Но если бы мы рассматривали точки, координаты которых являются комплексными числами, то полученное уравнение определяло бы пару пересекающихся прямых. Потому кривая с таким каноническим уравнением называется парой мнимых пересекающихся прямых.

I₃. . Ясно, что в этом случае уравнение (21.2) не имеет решения. Преобразуем его к виду . Ведя обозначения , окончательно получим: . Такой кривой на плоскости не существует. Но если рассматривать точки с комплексными координатами, то существуют точки, координаты которых удовлетворяют полученному уравнению. Кривая в этом случае носит название мнимого эллипса.

Мы рассмотрели всевозможные случаи для кривых эллиптического типа.

II. Кривая имеет гиперболический тип. Тогда ее первый инвариант отрицателен, и, в силу наших договоренностей, .

II₁. Предположим, что в уравнении (2) . Тогда его можно преобразовать к виду: . Введем обозначения: . Окончательно получим: . Кривая представляет собой гиперболу.

Если в уравнении (2) , то помножим обе части уравнения на , и сделаем замену неизвестных по формулам: Мы придем к предыдущему случаю, опять получим гиперболу.

II₂. 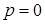. Уравнение (2) приводится к виду: . Если сделать замену: , то окончательно получим . Представим левую часть полученного уравнения в виде: . Кривая представляет собой пару пересекающихся прямых, имеющих соответственно уравнения: и .

Мы рассмотрели всевозможные случаи кривых, имеющих центр. Нетрудно установить, что во всех случаях начало канонической системы координат совпадает с центром кривой.

II. Кривая имеет параболический тип. Тогда, как отмечалось в предыдущем параграфе одно из собственных значении кривой равно нулю. Будем считать, что . Тогда уравнение (1) примет вид: . Без ограничения общности можно считать, что , иначе полученное уравнение следует умножить на . Преобразуем его к виду:

. (3)

II₁. . Преобразуем правую часть уравнение (21.3): . Осуществим параллельный перенос системы координат по формулам Уравнение (21.3) можно привести к виду: . Если ввести обозначения: , то окончательно получим: . Мы получили каноническое уравнение параболы при условии, что . Если , то следует поменять направление оси абсцисс, и мы также получим параболу.

Рассмотрим случай, при котором . Обозначим . Тогда уравнение (3) примет вид:

(4)

II₂. . Уравнение (4) можно представить как совокупность двух уравнений: и 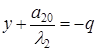. Поэтому кривая представляет собой две параллельные прямые с уравнениями: и 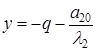. Прямые параллельны оси абсцисс.

II₃. . Уравнение (4) принимает вид: . Кривая представляет собой прямую, или, как говорят, пару совпавших параллельных прямых.

II₄. . Уравнение (4) не имеет решений. В этом случае говорят, что кривая является парой мнимых параллельных прямых.

Мы провели полную классификацию кривых второго порядка на плоскости. Таких кривых существует три типа: эллиптический, гиперболический и параболический и девять видов. Мы доказали следующую теорему.

Теорема. Если на плоскости задана кривая второго порядка, то она принадлежит одному из следующих трех типов и девяти видов.

№	Тип кривой	Название кривой	Каноническое уравнение
	Эллиптический	Эллипс
	Мнимый эллипс
	Пара мнимых пересекающихся прямых
	гиперболический	Гипербола
	Пара действительных пересекающихся прямых
	Параболический	Парабола
	Пара параллельных прямых
	Пара мнимых параллельных прямых
	Пара совпавших прямых

Пример 1. Привести к каноническому виду уравнение кривой: .

Решение. Если сравнить данное уравнение с общим уравнением кривой второго порядка, то в рассматриваемом случае

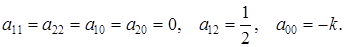
Поэтому характеристическое уравнение кривой приводится к виду: Оно имеет корни: Определим, на какой угол j следует повернуть исходную систему координат, чтобы в новой системе уравнение кривой имело вид (1). В новой системе координаты базисных векторов равны: и , они удовлетворяют системе:

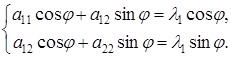
Для определения координат базисных векторов новой системы достаточно первое уравнение разделить на и решить полученное уравнение относительно , получим:

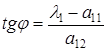. (5)

Можно воспользоваться вторым уравнением этой системы. Самостоятельно проверьте, что мы получим то же значение тангенса искомого угла. Определив тангенс угла, найдем его синус и косинус по известным из тригонометрии формулам: . При этом следует иметь в виду, что искомый угол j расположен в первой четверти. Для упрощения уравнения кривой следует произвести замену неизвестных по формулам поворота системы координат вокруг ее начала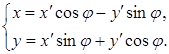

В рассматриваемом случае, согласно (5), . Искомый угол равен . Поэтому формулы поворота системы координат равны: Подставим их в уравнение данной кривой, получим: , или 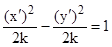. Данная кривая - гипербола. Кривая представляет собой гиперболу.

Поиск по сайту: