Асимптотически точная оценка функции роста

Если для функции T (n) найдутся константы c ₁ > 0 и c ₂ > 0 и такое число n ₀ > 0, что выполнится условие , то говорят что время выполнения алгоритма (программы) асимптотически точно соответствует функции n ². Этот факт обозначается как , где n – длина входа алгоритма.

Определение 1. Вообще, есл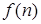и и положительно определенные функции, то запись означает, что найдутся константы c ₁ > 0 и c ₂ > 0 и такое n ₀ > 0, что для всех .

(Запись «» читается как «эф от эн есть тэта от же от эн»).

Если 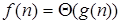, то говорят, что является асимптотически точной оценкой (asymptotically tight bound) для . На самом деле это отношение симметрично, если: 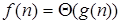, то .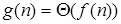

Рис. 2. Иллюстрация к определению

Заметим, что есть обозначение факта некоторого соотношения между двумя функциями, поэтому, если установлено , а следовательно и , то это вовсе не означает, что .

Проиллюстрируем свойство симметрии функции . Можно показать, что . Согласно определению надо указать положительные константы с₁, с₂ и число n₀ так, чтобы неравенства

выполнялись для всех 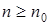. Разделим все части неравенства на n²:

.

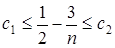Видно, что для выполнения второго неравенства достаточно положить c ₂ = 1/2. Первое будет выполнено, если (например) n ₀ = 7 и c ₁=1/14.

Покажем, что В самом деле, пусть найдутся такие c ₂и n ₀, что для всех . Но тогда для всех , из чего следует что c ₂ не может является константой, так как растет с увеличением n, что противоречит определению.

Упомянем важный частный случай использования -обозначений: , который обозначает ограниченную функцию, отделённую от нуля некоторый положительной константой при достаточно больших значениях аргумента.

Асимптотические обозначения часто употребляются внутри формул. Например, рекуррентное соотношение вида

означает, что время выполнения алгоритма для входа длины n определяется временем выполнения для входной последовательности из (n –1) элементов и некоторой функции, про которую нам важно знать лишь, что она не меньше c₁n и не больше c₂n для некоторых положительных с₁ и с₂ и для всех достаточно больших n, которая по определению обозначается через . Иными словами, время работы программы при изменение входной длины увеличивается пропорционально n, а в алгоритме этому члену в выражении соответствует фрагмент с асимптотической оценкой равной n.

Часто асимптотические обозначения употребляются не вполне формально, хотя их подразумеваемый смысл обычно ясен из контекста.

Типичный пример неформального использования асимптотических обозначений – цепочка равенств вида . Второе из этих равенств понимается при этом так: какова бы ни была функция 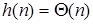в левой части, сумма есть .

Отыскивая асимптотически точную оценку для суммы, мы можем отбрасывать члены меньшего порядка, которые при больших n становятся малыми по сравнению с основным слагаемым. Заметим также, что коэффициент при старшем члене роли не играет (он может повлиять только на выбор констант с ₁и с ₂). Например, рассмотрим квадратичную функцию , где a, b, c – некоторые константы и a > 0. Отбрасывая члены младших порядков и коэффициент при старшем члене, находим что Чтобы убедиться в этом формально, можно положить с ₁ = a/ 4, c ₂ = 7 a/ 4и . Вообще, для любого полинома p(n) степени d с положительным старшим коэффициентом имеем .

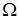1.3.2 - и - обозначения

Вообще, запись 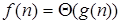включает в себя две оценки: верхнюю и нижнюю. Их можно разделить:

Определение 2. Пусть имеются функции и , которые принимают неотрицательные значения для достаточно больших значений аргумента. Говорят, что , если найдётся такая константа c > 0 и такое число n₀, что 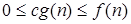для всех (рис. 3а).

Определение 3. Говорят, что 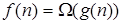, если найдётся такая константа c > 0 и такое число n₀, что 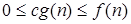для всех (рис. 3б). Эти записи читаются так: «эф от эн есть о большое от же от эн», «эф от эн есть омега большая от же от эн».

Теорема 1. Для любых двух функций и свойство выполнено тогда и только тогда, когда и .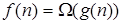

Замечание: Для любых двух функций и свойство и 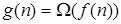равносильны.

(а) (б)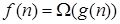
Рис. 3. Верхняя (а) и нижняя (б) асимптотические оценки функции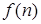

Асимптотические обозначения могут употребляются внутри формул. Например, мы можем написать выражение

имея в виду сумму h (1) + h (2) + … + h (n), где h (×) – некоторая функция, для которой h (i) = O (i). Можно показать, что сама эта сумма как функция от n есть O(n²).

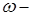1.3.3 и обозначения

Запись 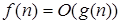означает, что с ростом n отношение остаётся ограниченным. Если к тому же

,

то мы пишем (читается «эф от эн есть о малое от же от эн»). Формально говоря, , если для всякого положительного найдётся такое n₀, что при всех . Тем самым запись предполагает, что и неотрицательны для достаточно больших n.

Пример: но

Аналогичным образом вводится 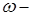обозначение: говорят, что есть («эф от эн есть омега малая от же от эн»), если для всякого положительного e найдется такое n ₀, что при всех , причем

.

Очевидно, 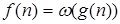равносильно

Пример: , но

Таким образом, может существовать три основных случая (существует и четвертый случай, когда предела не существует, однако он встречается довольно редко в реальной практике анализа алгоритмов):

Однако на практике строгими определениями пользуются редко. Существует более удобный метод выполнения этой оценки, основанный на мощном математическом аппарате, специально созданного для вычисления пределов отношения двух рассматриваемых функций, в частности правилом Лопиталя (L'Hopital):

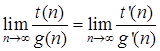
и формулой Стирлинга (Stirling) для достаточно больших n:

.

Пример 1. Сравните порядки роста функций f (n)= n (n – 1)/2 и g (n)= n ².

Решение: поскольку

предел равен положительной константе, обе функции имеют одинаковый порядок роста, что записывается как .

Пример 2. Сравните порядки роста функций и .

Решение:

.

Поскольку предел равен нулю, функция имеет меньший порядок роста, чем . То есть .

Пример 3. Сравните порядки роста функци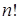й и .

Решение: воспользовавшись формулой Стерлинга, получим:

Следовательно, хотя функция 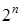растет очень быстро, функция 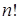растет еще быстрее, что записывается как 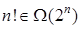. Обратим внимание, что при использовании этой формы записи, в отличие от случая использования пределов, не можем сделать однозначный вывод о том, что порядок роста функции 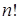выше, чем функции 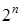, а не, скажем, равен ей, поэтому используется «большая» омега.

Поиск по сайту: