Основные классы эффективности

В теории анализа эффективности алгоритмов к одному классу относят все функции, чей порядок роста одинаков с точностью до постоянного множителя. Рассмотрим их более подробно.

Класс трудоемкости	Вид функции трудоемкости	Название подкласса	Примечание	Пример алгоритма данного подкласса
Полиномиальный класс (Р -класс)	const		Алгоритм не зависит от длины входных параметров, то есть число операторов постоянно и не измениться не при каком случае.
log n	логарифмический	Обычно такая зависимость появляется в результате сокращения размера задачи на постоянное значение на каждом шаге итерации алгоритма. Обратите внимание, что в логарифмическом алгоритме исключается работа со всеми входными данными	Алгоритм бинарного поиска (метод деления отрезка пополам) среди n элементов.
n	Линейная	К этому подклассу относятся алгоритмы, выполняющие сканирование списка, состоящего из n элементов.	Поиск элемента массива из n методом последовательного перебора
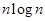
	«n - логарифм n»	К этому подклассу относятся большое количество алгоритмов декомпозиции, где для каждого из n элементов необходимо применить эффективный (например) поиск за логарифмическое время	Эффективные алгоритмы сортировки: пирамидальная, фиксированное двухпутевое слияния
n 2	Квадратичная	подобная зависимость характеризует эффективность алгоритмов, содержащих два вложенных цикла, каждый из которых выполняется не более n раз	Простые схемы сортировки, например, пузырьковая,
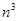
	Кубическая	Как правило, подобная зависимость характеризует эффективность алгоритмов, содержащих три вложенных цикла	Простой алгоритм перемножения матриц
Не детерминировано-полиномиальный (NP -класс)		Экспоненциальная	Данная зависимость типична для алгоритмов, выполняющих обработку всех подмножеств некоторого множества, состоящего из n элементов.	Задача о ханойских башнях.
n!	Факториальная	Данная зависимость типична для алгоритмов, выполняющих обработку всех перестановок некоторого множе­ства, состоящего из n элементов	Полный перебор всех сочетаний элементов исходного множества при поиске решения задачи.
Часто термин "экспоненциальный" используется в широком смысле (в том числе и для всего класса) и означает очень высокие порядки роста, имеющий принципиально другой характер поведения по сравнению с полиномом некоторой степени.

Для примера приведем числа, иллюстрирующие скорость роста для нескольких функций, которые часто используются при оценке временной сложности алгоритмов (см. Таблица 1).

Таблица 1

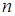
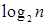
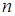
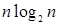
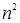
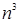
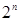
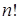
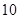
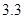
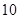
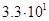
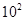
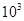
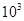
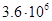
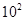
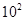
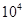
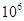
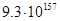
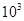
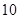
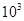
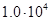
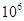
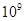
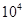
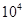
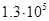
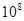
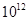
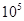
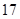
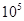
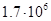
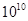
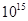
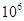
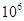
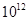
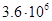
Порядок чисел, приведенных в таблице, имеет чрезвычайное значение для анализа алгоритмов. Как видно из таблицы, самый малый порядок роста имеет логарифмическая функция. Причем его значение настолько мало, что программы, реализующие алгоритмы с логарифмическим количеством основных операций, будут выполняться практически мгновенно для всех диапазонов входных данных реального размера, причем вне зависимости от основания логарифма, так как переход от одного основания к другому есть константа:

log _a n = log_a b log _b n.

Поэтому далее будем опускать основание логарифма, то есть log n.

Если считать, что числа соответствуют микросекундам, то для задачи с 1048476 элементами алгоритму со временем работы T (log n) потребуется 20 микросекунд, а алгоритму со временем работы T (n ²) – более 12 дней.

Существует и другая крайность: показательная функция 2ⁿ и функция n! – вычисление факториала. Обе эти функции имеют настолько высокий порядок роста, что его значение становится астрономически большим уже при умеренных зна­чениях n. Например, чтобы выполнить 2¹⁰⁰ операций компьютеру, имеющему производительность в один триллион операций в секунду, понадобиться без малого 4 • 1010 лет! Однако это ничто по сравнению со временем, которое затратит тот же компьютер на выполнение 100! операций.

Подводя итог, отметим: c помощью алгоритмов, в которых количество выполняемых операций растет по экспоненциальному закону, можно решить лишь задачи очень малых размеров.

Именно для этого и следует на практике оценивать трудоемкость разрабатываемого алгоритма.

Поиск по сайту: