Бесконечно большие функции и их связь с

бесконечно малыми.

Определение. Предел функции f(x) при х®а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число D>0, что неравенство

ïf(x)ï>M

выполняется при всех х, удовлетворяющих условию

0 < ïx - aï < D

Записывается .

Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим:

а если заменить на f(x)<M, то:

Графически приведенные выше случаи можно проиллюстрировать следующим образом:

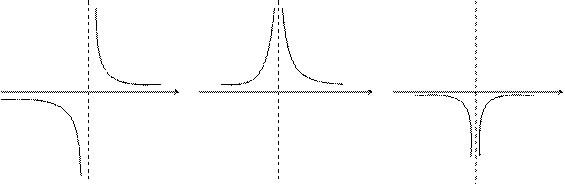a x a x a x

Определение. Функция называется бесконечно большой при х®а, где а – чосли или одна из величин ¥, +¥ или -¥, если 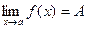, где А – число или одна из величин ¥, +¥ или -¥.

Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.

Теорема. Если f(x)®0 при х®а (если х®¥) и не обращается в ноль, то

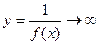
Сравнение бесконечно малых функций.

Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.

Например, функция f(x) = x¹⁰ стремится к нулю быстрее, чем функция f(x) = x.

Определение. Если 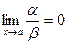, то функция a называется бесконечно малой более высокого порядка, чем функция b.

Определение. Если , то a и b называются бесконечно малыми одного порядка.

Определение. Если то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.

Пример. Сравним бесконечно малые при х®0 функции f(x) = x¹⁰ и f(x) = x.

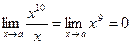
т.е. функция f(x) = x¹⁰ – бесконечно малая более высокого порядка, чем f(x) = x.

Определение. Бесконечно малая функция a называется бесконечно малой порядка k относительно бесконечно малой функции b, если предел конечен и отличен от нуля.

Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение не имеет предела, то функции несравнимы.

Пример. Если , то при х®0 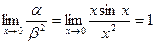, т.е. функция a - бесконечно малая порядка 2 относительно функции b.

Пример. Если , то при х®0 не существует, т.е. функция a и b несравнимы.

Свойства эквивалентных бесконечно малых.

1) a ~ a,

2) Если a ~ b и b ~ g, то a ~ g,

3) Если a ~ b, то b ~ a,

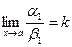4) Если a ~ a₁ и b ~ b₁ и , то и или .

Следствие: а) если a ~ a₁ и , то и

б) если b ~ b₁ и , то

Свойство 4 особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене их на эквивалентные бесконечно малые. Этот факт дает возможность при нахождении пределов заменять бесконечно малые на эквивалентные им функции, что может сильно упростить вычисление пределов.

Пример. Найти предел

Так как tg5x ~ 5x и sin7x ~ 7x при х ® 0, то, заменив функции эквивалентными бесконечно малыми, получим:

Пример. Найти предел .

Так как 1 – cosx = при х®0, то .

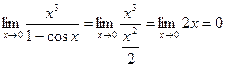Пример. Найти предел

Если a и b - бесконечно малые при х®а, причем b - бесконечно малая более высокого порядка, чем a, то g = a + b - бесконечно малая, эквивалентная a. Это можно доказать следующим равенством .

Тогда говорят, что a - главная часть бесконечно малой функции g.

Пример. Функция х² +х – бесконечно малая при х®0, х – главная часть этой функции. Чтобы показать это, запишем a = х², b = х, тогда

.

Некоторые замечательные пределы.

Первый замечательный предел. , где P(x) = a₀xⁿ + a₁x^n-1 +…+a_n,

Q(x) = b₀x^m + b₁x_m-1 +…+b_m - многочлены.

Итого:

Второй замечательный предел.

Третий замечательный предел.

Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.

Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:

Пример. Найти предел.

Пример. Найти предел.

Пример. Найти предел.

Пример. Найти предел.

Пример. Найти предел.

Пример. Найти предел .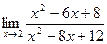

Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.

x² – 6x + 8 = 0; x² – 8x + 12 = 0;

D = 36 – 32 = 4; D = 64 – 48 = 16;

x₁ = (6 + 2)/2 = 4; x₁ = (8 + 4)/2 = 6;

x₂ = (6 – 2)/2 = 2; x₂ = (8 – 4)/2 = 2;

Тогда

Пример. Найти предел.

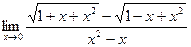домножим числитель и знаменатель дроби на сопряженное выражение: =

= .

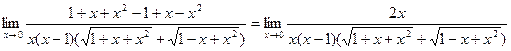Пример. Найти предел.

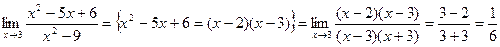
Пример. Найти предел .

Разложим числитель и знаменатель на множители.

x² – 3x + 2 = (x – 1)(x – 2)

x³ – 6x² + 11x – 6 = (x – 1)(x – 2)(x – 3), т.к.

x³ – 6x² + 11x – 6 x - 1

x³ – x² x² – 5x + 6

- 5x² + 11x

- 5x² + 5x

6x - 6

6x - 6 0

x² – 5x + 6 = (x – 2)(x – 3)

Тогда

Пример. Найти предел.

Для самостоятельного решения:

1)

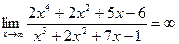
2)

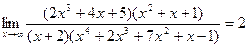
3)

4)

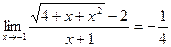
5)

6)

7)

8) - не определен.

Непрерывность функции в точке.

Определение. Функция f(x), определенная в окрестности некоторой точки х₀, называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т.е.

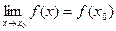
Тот же факт можно записать иначе:

Определение. Если функция f(x) определена в некоторой окрестности точки х₀, но не является непрерывной в самой точке х₀, то она называется разрывной функцией, а точка х₀ – точкой разрыва.

Пример непрерывной функции:

y

f(x₀)+e

f(x₀)

f(x₀)-e

0 x₀-D x₀ x₀+D x

Пример разрывной функции:

y

f(x₀)+e

f(x₀)

f(x₀)-e

x₀ x

Определение. Функция f(x) называется непрерывной в точке х₀, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию

верно неравенство .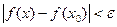

Определение. Функция f(x) называется непрерывной в точке х = х₀, если приращение функции в точке х₀ является бесконечно малой величиной.

f(x) = f(x₀) + a(x)

где a(х) – бесконечно малая при х®х₀.

Свойства непрерывных функций.

1) Сумма, разность и произведение непрерывных в точке х₀ функций – есть функция, непрерывная в точке х₀.

2) Частное двух непрерывных функций – есть непрерывная функция при условии, что g(x) не равна нулю в точке х₀.

3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х₀, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.

Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.

Непрерывность некоторых элементарных функций.

1) Функция f(x) = C, C = const – непрерывная функция на всей области определения.

2) Рациональная функция 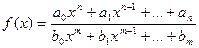непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.

3) Тригонометрические функции непрерывны на своей области определения.

Докажем свойство 3 для функции y = sinx.

Запишем приращение функции Dy = sin(x + Dx) – sinx, или после преобразования:

Действительно, имеется предел произведения двух функций и . При этом функция косинус – ограниченная функция при Dх®0 , а т.к.

предел функции синус 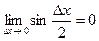, то она является бесконечно малой при Dх®0.

Таким образом, имеется произведение ограниченной функции на бесконечно малую, следовательно это произведение, т.е. функция Dу – бесконечно малая. В соответствии с рассмотренными выше определениями, функция у = sinx – непрерывная функция для любого значения х = х₀ из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.

Аналогично можно доказать непрерывность остальных тригонометрических функций на всей области определения.

Вообще следует заметить, что все основные элементарные функции непрерывны на всей своей области определения.

Точки разрыва и их классификация.

Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х₀, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х₀ является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если односторонний предел (см. выше) , то функция называется непрерывной справа.

х₀

Если односторонний предел (см. выше) , то функция называется непрерывной слева.

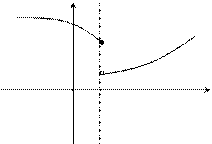х₀

Определение. Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

Определение. Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х₀, достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Определение. Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)

не является непрерывной в любой точке х₀.

Пример. Функция f(x) = имеет в точке х₀ = 0 точку разрыва 2 – го рода, т.к.

.

Пример. f(x) =

Функция не определена в точке х = 0, но имеет в ней конечный предел , т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:

График этой функции:

Пример. f(x) = =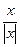

y

0 x

-1

Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.

Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.

Непрерывность функции на интервале и на отрезке.

Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).

При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.

Свойства функций, непрерывных на отрезке.

Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M £ f(x) £ M.

Доказательство этого свойства основано на том, что функция, непрерывная в точке х₀, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х₀, то образуется некоторая окрестность точки х₀.

Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.

Т.е. существуют такие значения х₁ и х₂, что f(x₁) = m, f(x₂) = M, причем

m £ f(x) £ M

Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).

Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.

Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.

Свойство 4: Если функция f(x) непрерывна в точке х = х₀, то существует некоторая окрестность точки х₀, в которой функция сохраняет знак.

Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.

Т.е. если sign(f(a)) ¹ sign(f(b)), то $ х₀: f(x₀) = 0.

Определение. Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого e>0 существует D>0 такое, что для любых точек х₁Î[a,b] и x₂Î[a,b] таких, что

ïх₂ – х₁ï< D

верно неравенство ïf(x₂) – f(x₁)ï < e

Отличие равномерной непрерывности от “обычной” в том, что для любого e существует свое D, не зависящее от х, а при “обычной” непрерывности D зависит от e и х.

Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.

(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)

Пример.

Функция непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т.к. существует такое число D>0 такое, что существуют значения х₁ и х₂ такие, чтоïf(x₁) – f(x₂)ï>e, e - любое число при условии, что х₁ и х₂ близки к нулю.

Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

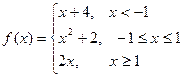
в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода

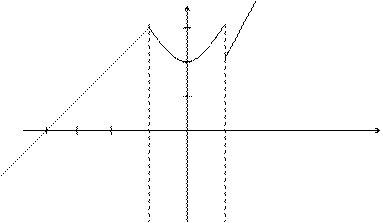у

-4 -1 0 1 х

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

в точке х = 0 функция непрерывна в точке х = 1 точка разрыва 1 – го рода

у

-p -p/2 0 1 x

Комплексные числа.

Определение. Комплексным числом z называется выражение , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:

При этом число a называется действительной частью числа z (a = Re z), а b - мнимой частью (b = Im z).

Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.

Определение. Числа и называются комплексно – сопряженными.

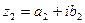Определение. Два комплексных числа и называются равными, если соответственно равны их действительные и мнимые части:

Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.

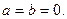
Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.

Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.

у

A(a, b)

r b

j

0 a x

Таким образом, на оси ОХ располагаются действительные числа, а на оси ОY – чисто мнимые.

С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.

Тригонометрическая форма числа.

Из геометрических соображений видно, что . Тогда комплексное число можно представить в виде:

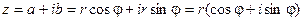
Такая форма записи называется тригонометрической формой записи комплексного числа.

При этом величина r называется модулем комплексного числа, а угол наклона j - аргументом комплексного числа.

.

Из геометрических соображений видно:

Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы.

Действия с комплексными числами.

Основные действия с комплексными числами вытекают из действий с многочленами.

1) Сложение и вычитание.

2) Умножение.

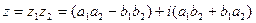
В тригонометрической форме:

,

С случае комплексно – сопряженных чисел:

3) Деление.

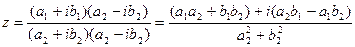
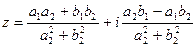
В тригонометрической форме:

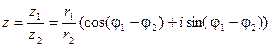
4) Возведение в степень.

Из операции умножения комплексных чисел следует, что

В общем случае получим:

,

где n – целое положительное число.

Это выражение называется формулой Муавра.

(Абрахам де Муавр (1667 – 1754) – английский математик)

Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.

Пример. Найти формулы sin2j и cos2j.

Рассмотрим некоторое комплексное число

Тогда с одной стороны .

По формуле Муавра: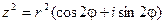

Приравнивая, получим

Т.к. два комплексных числа равны, если равны их действительные и мнимые части, то

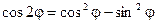
Получили известные формулы двойного угла.

5) Извлечение корня из комплексного числа.

Возводя в степень, получим:

Отсюда:

Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.

Показательная форма комплексного числа.

Рассмотрим показательную функцию

Можно показать, что функция w может быть записана в виде:

Данное равенство называется уравнением Эйлера. Вывод этого уравнения будет рассмотрен позднее. (См.).

Для комплексных чисел будут справедливы следующие свойства:

1)

2)

3) где m – целое число.

Если в уравнении Эйлера показатель степени принять за чисто мнимое число (х=0), то получаем:

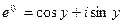
Для комплексно – сопряженного числа получаем:

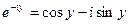
Из этих двух уравнений получаем:

Этими формулами пользуются для нахождения значений степеней тригонометрических функций через функции кратных углов.

Если представить комплексное число в тригонометрической форме:

и воспользуемся формулой Эйлера:

Полученное равенство и есть показательная форма комплексного числа.

Разложение многочлена на множители.

Определение. Функция вида f(x) называется целой рациональной функцией от х.

Теорема Безу. (Этьенн Безу (1730 – 1783) – французский математик)

При делении многочлена f(x) на разность x – a получается остаток, равный f(a).

Доказательство. При делении многочлена f(x) на разность x – a частным будет многочлен f₁(x) степенина единицу меньшей, чем f(x), а остатком – постоянное число R.

Переходя к пределу при х ® a, получаем f(a) = R.

Следствие. Если, а – корень многочлена, т.е. f(a) = 0, то многочлен f(x) делится на (х – а) без остатка.

Определение. Если уравнение имеет вид Р(х) = 0, где Р(х) – многочлен степени n, то это уравнение называется алгебраическим уравнением степени n.

Теорема. (Основная теорема алгебры) Всякая целая рациональная функция f(x) имеет, по крайней мере, один корень, действительный или комплексный.

Теорема. Всякий многочлен n – ой степени разлагается на n линейных множителей вида (x – a) и множитель, равный коэффициенту при xⁿ.

Теорема. Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого.

Если среди корней многочлена встречаются кратные корни, то разложение на множители имеет вид:

k_i - кратность соответствующего корня.

Отсюда следует, что любой многочлен n – ой степени имеет ровно n корней (действительных или комплексных).

Это свойство имеет большое значение для решения алгебраических уравнений, дифференциальных уравнений и играет важную роль в анализе функций.

Рассмотрим несколько примеров действий с комплексными числами.

Пример. Даны два комплексных числа 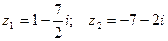. Требуется а) найти значение выражения в алгебраической форме, б) для числа найти тригонометрическую форму, найти z²⁰, найти корни уравнения

a) Очевидно, справедливо следующее преобразование:

Далее производим деление двух комплексных чисел:

Получаем значение заданного выражения: 16(- i)⁴ = 16 i ⁴ =16.

б) Число представим в виде , где

Тогда .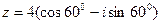

Для нахождения воспльзуемся формулой Муавра.

Если , то

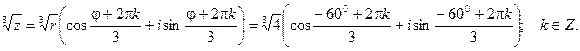
Элементы высшей алгебры.

Основные понятия теории множеств.

Определение. Множеством М называется объединение в единое целое определенных различимых объектов а, которые называются элементами множества.

а Î М

Множество можно описать, указав какое – нибудь свойство, присущее всем элементам этого множества.

Множество, не содержащее элементов, называется пустым и обзначается Æ.

Определение. Если все элементы множества А являются также элементами множества В, то говорят, что множество А включается (содержится) в множестве В.

А

В

А Ì В

Определение. Если А Í В, то множество А называется подмножеством множества В, а если при этом А ¹ В, то множество А называется собственным подмножеством множества В и обозначается А Ì В.

Для трех множеств А, В, С справедливы следующие соотношения.

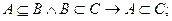
Связь между включением и равенством множеств устанавливается следующим соотношением:

Здесь знак Ù обозначает конъюнкцию (логическое “и”).

Операции над множествами.

Определение. Объединением множеств А и В называется множество С, элементы которого принадлежат хотя бы одномк из множеств А и В.

Обозначается С = А È В.

А

В

Геометрическое изображение множеств в виде области на плоскости называется диаграммой Эйлера – Венна.

Определение. Пересечением множеств А и В называется множество С, элементы которого принадлежат каждому из множеств А и В.

Обозначение С = А Ç В.

А С В

Для множеств А, В и С справедливы следующие свойства:

А Ç А = А È А = А; A È B = B È A; A Ç B = B Ç A;

(A Ç B) Ç C = A Ç (B Ç C); (A È B) È C = A È (B È C);

A È (B Ç C) = (A È B) Ç (A È C); A Ç (B È C) = (A Ç B) È (A Ç C);

A È (A Ç B) = A; A Ç (A È B) = A;

Æ = А; A Ç Æ = Æ;

Определение. Разностью множеств А и В называется множество, состоящее из элементов множества А, не принадлежащих множеству В.

Обозначается С = А \ В.

А В

Определение. Симметрической разностью множеств А и В называется множество С, элементы которого принадлежат в точности одному из множеств А или В.

Обозначается А D В.

А D В = (A \ B) È (B \ A)

A B

Определение. С_Е называется дополнением множества А относительно множества Е, если А Í Е и C_Е = Е \ A.

A E

Для множеств А, В и С справедливы следующие соотношения:

A \ B Í A; A \ A = Æ; A \ (A \ B) = A Ç B;

A D B = B D A; A D B = (A È B) \ (A Ç B);

A \ (B È C) = (A \ B) Ç (A \ C); A \ (B Ç C) = (A \ B) È (A \ C);

(A È B) \ C = (A \ C) È (B \ C); (A Ç B) \ C = (A \ C) Ç (B \ C);

A \ (B \ C) = (A \ B) È (A Ç C); (A \ B) \ C = A \ (B È C);

(A D B) D C = A D (B D C); A Ç (B D C) = (A Ç B) D (A Ç C);

A È C_EA = E; A Ç C_EA = Æ; C_EE = Æ; C_EÆ = E; C_EC_EA = A;

C_E(A È B) = C_EA Ç C_EB; C_E(A Ç B) = C_EA È C_EB;

Пример. Исходя из определения равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграммы Эйлера - Вейна.

Из записанных выше соотношений видно, что

Æ = A \ В

Что и требовалось доказать.

Для иллюстрации полученного результата построим диаграммы Эйлера – Вейна

А В А В

AÇB

Пример. Исходя из определения равенства множеств и операций над множествами, доказать тождество.

A \ (B È C) = (A \ B) Ç (A \ C)

Если некоторый элемент х Î А \ (В È С), то это означает, что этот элемент принадлежит множеству А, но не принадлежит множествам В и С.

Множество А \ В представляет собой множество элементов множества А, не принадлежащих множеству В.

Множество А \ С предсталяет собой множество элементов множества А, не принадлежащих множеству С.

Множество (A \ B) Ç (A \ C) представляет собой множество элементов, которые принадлежат множеству А, но не принадлежат ни множеству В, ни множеству С.

Таким образом, тождество можно считать доказанным.

Отношения и функции.

Определение. Упорядоченной парой (a, b) двух элементов a и b называется множество {{ a },{a, b}}.

Для любых элементов a, b, c, d справедливо соотношение:

Определение. Декартовым произведением множеств А и В называется множество всех упорядоченных пар (a, b), где а ÎА, b ÎB.

Декартово произведение п равных множеств А будет называться п – й декартовой степенью множества А и обозначаться Аⁿ.

Определение. n – мерным отношением R на непустом множестве А называется подмножество Аⁿ. Если R – n – мерное отношение на множестве А и (а₁,а₂,…а_n) ÎR, то говорят, что отношение R выполняется для элементов а₁,а₂,…а_n и записывают R а₁а₂…а_n. Если n = 2, то такое отношение называется бинарным.

Для бинарного отношения вместо общей записи R a₁a₂ применяют запись а₁Ra₂.

Свойства бинарных отношений.

Определение. Произведением двух бинарных отношений R и S, заданных на множестве А, называется множество

Знак | называется штрих Шеффера и обозначает антиконъюнкцию.

Определение. Обратным (инверсным) отношением к отношению R, заданному на множестве А, называется отношение R^-1, определяемое равенством:

Если R, S и T – бинарные отношения на множестве А, то выполняются следующие равентсва:

Алгебраические структуры.

Определение. На множестве А определена алгебраическая операция, если каждым двум элементам этого множества, взятым в определенном порядке, однозначным образом поставлен в соответствие некоторый третий элемент из этого же множества.

Примерами алгебраических операций могут служить такие операции как сложение и вычитание целых чисел, сложение и вычитание векторов, матриц, умножение квадратных матриц, векторное умножение векторов и др.

Отметим, что скалярное произведение векторов не может считаться алгебраической операцией, т.к. результатом скалярного произведения будет число, и числа не относятся к множеству векторов, к которому относятся сомножители.

Определение. Множество А с определенной на нем алгебраической операцией (например, умножением) называется группой, если выполнены следующие условия:

1) для любых трех элементов a, b, c Î A выполняется свойство ассоциативности:

2) в множестве А существует такой элемент е, что для любого элемента а из этого множества выполняется равенcтво:

3) для любого элемента а множества существует элемент а’ из этого же множества такой, что

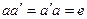
Различные множества могут являться группой относительно какой- либо операции и не являться группой относительно другой операции.

Число элементов называется порядком группы.

Определение. Между элементами множеств M и N установлено взаимно однозначное соответствие, если каждому элементу множества М поставлен в соответствие определенный элемент множества N, причем различным элементам одного множества соответсвуют различные элементы другого множества.

Определение. Две группы M и N называются изоморфными, если между их элементами можно установить взаимно однозначное соответсвие, при котором для любых двух элементов a, bÎ M и соответствующим им элементам a’, b’Î N элементу

с = ab будет соответствует элемент c’ = a’b’.

При этом отображение группы М на группу N называется гомоморфизмом.

Определение. Если операция, определенная в группе коммутативна, (т.е. для любых элементов a и b группы верно соотношение ab=ba), то такая группа называется коммутативной или абелевой группой.

Определение. Множество R с двумя определенными в нем алгебраическими операциями, сложением и умножением, называется кольцом, если относительно операции сложения оно является абелевой группой, а операция умножения дистрибутивна, т.е. для любых элементов a, b и с Î R справедливы равенства:

Если операция умножения, определенная в кольце коммутативна, то такое кольцо называется коммутативным кольцом.

Определение. Полем называется коммутативное кольцо, в котором для любого ненулевого элемента a¹ 0 и любого элемента b существует единственный элемент х такой, что ax = b.

Дискретная математика.

Элементы комбинаторики.

Если из некоторого количества элементов, различных меду собой, составлять различные комбинации, то среди них можно выделить три типа комбинаций, носящих общее название – соединения.

Рассмотрим подробнее эти три типа соединений:

1) Перестановки.

Определение. Если в некотором множестве 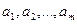переставлять местами элементы, оставляя неизменным их количество, то каждая полученная таким образом комбинация называется перестановкой.

Общее число перестановок из m элементов обозначается P_m и вычисляется по формуле:

2) Размещения.

Определение. Если составлять из т различных элементов группы по n элементов в каждой, располагая взятые элементы в различном порядке. Получившиеся при этом комбинации называются размещениями из т элементов по п.

Общее число таких размещений расчитывается по формуле:

Вообще говоря, перестановки являются частным случаем размещений.

3) Сочетания.

Определение. Если из т элементов составлять группы по п элементов в каждой, не обращая внимания на порядок элементов в группе, то получившиеся при этом комбинации называются сочетаниями из т элементов по п.

Общее число сочетаний находится по формуле:

Также одним из вариантов комбинаций являются перестановки с повторяющимися элементами.

Если среди т элементов имеется т₁ одинаковых элементов одного типа, т₂ одинаковых элементов другого типа и т.д., то при перестановке этих элементов всевозможными способами получаем комбинации, количество которых определяется по формуле:

Пример. Номер автомобиля состоит из трех букв и трех цифр. Сколько различных номеров можно составить, используя 10 цифр и алфавит в 30 букв.

Очевидно, что количество всех возможных комбинаций из 10 цифр по 4 равно 10.000.

Число всех возможных комбинаций из 30 букв по две равно .

Если учесть возможность того, что буквы могут повторяться, то число повторяющихся комбинаций равно 30 (одна возможность повтора для каждой буквы). Итого, полное количество комбинаций по две буквы равно 900.

Если к номеру добавляется еще одна буква из алфавита в 30 букв, то количество комбинаций увеличивается в 30 раз, т.е. достигает 27.000 комбинаций.

Окончательно, т.к. каждой буквенной комбинации можно поставить в соответствие числовую комбинацию, то полное количество автомобильных номеров равно 270.000.000.

Бином Ньютона. (полиномиальная формула)

В дальнейшем будет получена формула бинома Ньютона с помощью приемов дифференциального исчисления.

Бином Ньютона – это формула, выражающая выражение (a + b)ⁿ в виде многочлена. Эта формула имеет вид:

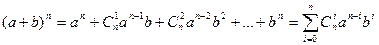
- число сочетаний из п элементов по k.

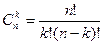
Широко известные формулы сокращенного умножения квадрата суммы и разности, куба суммы и разности, являются частными случаями бинома Ньютона.

Поиск по сайту: