Приведение квадратичных форм к каноническому

виду.

Рассмотрим некоторое линейное преобразование А с матрицей .

Это симметрическое преобразование можно записать в виде:

y₁ = a₁₁x₁ + a₁₂x₂

y₂ = a₁₂x₁ + a₂₂x₂

где у₁ и у₂ – координаты вектора в базисе .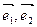

Очевидно, что квадратичная форма может быть записана в виде

Ф(х₁, х₂) = х₁у₁ + х₂у₂.

Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х₁ и х₂ – скалярное произведение .

Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.

Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:

.

При переходе к новому базису от переменных х₁ и х₂ мы переходим к переменным и . Тогда:

Тогда .

Выражение называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.

Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.

Пример. Привести к каноническому виду квадратичную форму

Ф(х₁, х₂) = 27 .

Коэффициенты: а₁₁ = 27, а₁₂ = 5, а₂₂ = 3.

Составим характеристическое уравнение: ;

(27 - l)(3 - l) – 25 = 0

l² - 30l + 56 = 0

l₁ = 2; l₂ = 28;

Пример. Привести к каноническому виду уравнение второго порядка:

17x² + 12xy + 8y² – 20 = 0.

Коэффициенты а₁₁ = 17, а₁₂ = 6, а₂₂ = 8. А =

Составим характеристическое уравнение:

(17 - l)(8 - l) - 36 = 0

136 - 8l - 17l + l² – 36 = 0

l² - 25l + 100 = 0

l₁ = 5, l₂ = 20.

Итого: - каноническое уравнение эллипса.

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение: Составим характеристическое уравнение квадратичной формы : при

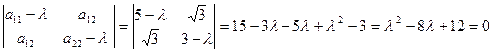
Решив это уравнение, получим l₁ = 2, l₂ = 6.

Найдем координаты собственных векторов:

полагая m₁ = 1, получим n₁ =

полагая m₂ = 1, получим n₂ =

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

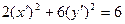
Каноническое уравнение линии в новой системе координат будет иметь вид:

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение: Составим характеристическое уравнение квадратичной формы : при

Решив это уравнение, получим l₁ = 1, l₂ = 11.

Найдем координаты собственных векторов:

полагая m₁ = 1, получим n₁ =

полагая m₂ = 1, получим n₂ =

Собственные векторы: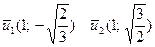

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

4ху + 3у² + 16 = 0

Коэффициенты: a₁₁ = 0; a₁₂ = 2; a₂₂ = 3.

Характеристическое уравнение:

Корни: l₁ = -1, l₂ = 4.

Для l₁ = -1 Для l₂ = 4

m₁ = 1; n₁ = -0,5; m₂ = 1; n₂ = 2;

= (1; -0,5) = (1; 2)

Получаем: -каноническое уравнение гиперболы.

При использовании компьютерной версии “ Курса высшей математики ” возможно запустить программу, которая решает рассморенные выше примеры для любых начальных условий.

Для запуска программы дважды щелкните на значке:

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

Введение в математический анализ.

Числовая последовательность.

Определение. Если каждому натуральному числу n поставлено в соответствие число х_n, то говорят, что задана последовательность

x_1, х₂, …, х_n = {x_n}

Общий элемент последовательности является функцией от n.

x_n = f(n)

Таким образом последовательность может рассматриваться как функция.

Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.

Пример. {x_n} = {(-1)ⁿ} или {x_n} = -1; 1; -1; 1; …

{x_n} = {sinpn/2} или {x_n} = 1; 0; 1; 0; …

Для последовательностей можно определить следующие операции:

1) Умножение последовательности на число m: m{x_n} = {mx_n}, т.е. mx₁, mx₂, …

2) Сложение (вычитание) последовательностей: {x_n} ± {y_n} = {x_n ± y_n}.

3) Произведение последовательностей: {x_n}×{y_n} = {x_n×y_n}.

4) Частное последовательностей: при {y_n} ¹ 0.

Ограниченные и неограниченные последовательности.

Определение. Последовательность {x_n} называется ограниченной, если существует такое число М>0, что для любого n верно неравенство:

т.е. все члены последовательности принадлежат промежутку (-М; M).

Определение. Последовательность {x_n}называется ограниченной сверху, если для любого n существует такое число М, что

x_n £ M.

Определение. Последовательность {x_n}называется ограниченной снизу, если для любого n существует такое число М, что

x_n ³ M

Пример. {x_n} = n – ограничена снизу {1, 2, 3, … }.

Определение. Число а называется пределом последовательности {x_n}, если для любого положительного e>0 существует такой номер N, что для всех n > N выполняется условие:

Это записывается: lim x_n = a.

В этом случае говорят, что последовательность {x_n} сходится к а при n®¥.

Свойство: Если отбросить какое- либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример. Доказать, что предел последовательности lim .

Пусть при n > N верно , т.е. . Это верно при , таким образом, если за N взять целую часть от , то утверждение, приведенное выше, выполняется.

Пример. Показать, что при n®¥ последовательность 3, имеет пределом число 2.

Итого: {x_n}= 2 + 1/n; 1/n = x_n – 2

Очевидно, что существует такое число n, что 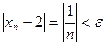, т.е. lim {x_n} = 2.

Теорема. Последовательность не может иметь более одного предела.

Доказательство. Предположим, что последовательность {x_n}имеет два предела a и b, не равные друг другу.

x_n ® a; x_n ® b; a ¹ b.

Тогда по определению существует такое число e >0, что

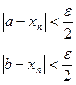
Запишем выражение:

А т.к. e- любое число, то , т.е. a = b. Теорема доказана.

Теорема. Если x_n ® a, то .

Доказательство. Из x_n ® a следует, что . В то же время:

, т.е. , т.е. . Теорема доказана.

Теорема. Если x_n ® a, то последовательность {x_n} ограничена.

Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.

Например, последовательность не имеет предела, хотя

Монотонные последовательности.

Определение. 1) Если x_n+1 > x_n для всех n, то последовательность возрастающая.

2)Если x_n+1 ³ x_n для всех n, то последовательность неубывающая.

3)Если x_n+1 < x_n для всех n, то последовательность убывающая.

4)Если x_n+1 £ x_n для всех n, то последовательность невозрастающая

Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.

Пример. {x_n} = 1/n – убывающая и ограниченная

{x_n} = n – возрастающая и неограниченная.

Пример. Доказать, что последовательность {x_n}= монотонная возрастающая.

Найдем член последовательности {x_n+1}=

Найдем знак разности: {x_n}-{x_n+1}=

, т.к. nÎN, то знаменатель положительный при любом n.

Таким образом, x_n+1 > x_n. Последовательность возрастающая, что и следовало доказать.

Пример. Выяснить является возрастающей или убывающей последовательность

{x_n} = .

Найдем . Найдем разность

, т.к. nÎN, то 1 – 4n <0, т.е. х_n+1 < x_n. Последовательность монотонно убывает.

Следует отметить, что монотонные последовательности ограничены по крайней мере с одной стороны.

Теорема. Монотонная ограниченная последовательность имеет предел.

Доказательство. Рассмотрим монотонную неубывающую последовательность

х₁ £ х₂ £ х₃ £ … £ х_n £ x_n+1 £ …

Эта последовательность ограничена сверху: x_n £ M, где М – некоторое число.

Т.к. любое, ограниченное сверху, числовое множество имеет четкую верхнюю грань, то для любого e>0 существует такое число N, что x_N > a - e, где а – некоторая верхняя грань множества.

Т.к. {x_n}- неубывающая последовательность, то при N > n а - e < x_N £ x_n,

x_n > a - e.

Отсюда a - e < x_n < a + e

-e < x_n – a < e или ôx_n - aô< e, т.е. lim x_n = a.

Для остальных монотонных последовательностей доказательство аналогично.

Теорема доказана.

Число е.

Рассмотрим последовательность {x_n} = .

Если последовательность {x_n} монотонная и ограниченная, то она имеет конечный предел.

По формуле бинома Ньютона:

или, что то же самое

Покажем, что последовательность {x_n} – возрастающая. Действительно, запишем выражение x_n+1 и сравним его с выражением x_n:

Каждое слагаемое в выражении x_n+1 больше соответствующего значения x_n, и, кроме того, у x_n+1 добавляется еще одно положительное слагаемое. Таким образом, последовательность {x_n} возрастающая.

Докажем теперь, что при любом n ее члены не превосходят трех: x_n < 3.

Итак, последовательность - монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.

Из неравенства 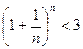следует, что е £ 3. Отбрасывая в равенстве для {x_n} все члены, начиная с четвертого, имеем:

переходя к пределу, получаем

Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа е.

Можно показать, что число е иррациональное и его значение равно 2,71828…

Аналогично можно показать, что , расширив требования к х до любого действительного числа:

Предположим:

Найдем

Число е является основанием натурального логарифма.

Выше представлен график функции y = lnx.

Связь натурального и десятичного логарифмов.

Пусть х = 10^у, тогда lnx = ln10^y, следовательно lnx = yln10

у = , где М = 1/ln10» 0,43429…- модуль перехода.

Предел функции в точке.

y f(x)

A + e

A

A - e

0 a - D a a + D x

Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)

Определение. Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х таких, что

0 < ïx - aï < D

верно неравенство ïf(x) - Aï< e.

То же определение может быть записано в другом виде:

Если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.

Запись предела функции в точке: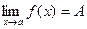

Определение. Если f(x) ® A₁ при х ® а только при x < a, то - называется пределом функции f(x) в точке х = а слева, а если f(x) ® A₂ при х ® а только при x > a, то называется пределом функции f(x) в точке х = а справа.

у

f(x)

А₂

А₁

0 a x

Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы А₁ и А₂ называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).

Предел функции при стремлении аргумента к бесконечности.

Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство

При этом предполагается, что функция f(x) определена в окрестности бесконечности.

Записывают: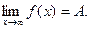

Графически можно представить:

y y

A A

0 0

x x

y y

A A

0 0

x x

Аналогично можно определить пределы для любого х>M и

для любого х<M.

Основные теоремы о пределах.

Теорема 1. , где С = const.

Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.

Теорема 2.

Доказательство этой теоремы будет приведено ниже.

Теорема 3.

Следствие.

Теорема 4. при

Теорема 5. Если f(x)>0 вблизи точки х = а и 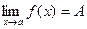, то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.

Теорема 6. Если g(x) £ f(x) £ u(x) вблизи точки х = а и 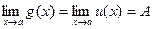, то и .

Определение. Функция f(x) называется ограниченной вблизи точки х = а, если существует такое число М>0, что ïf(x)ï<M вблизи точки х = а.

Теорема 7. Если функция f(x) имеет конечный предел при х®а, то она ограничена вблизи точки х = а.

Доказательство. Пусть 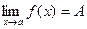, т.е. , тогда

или

, т.е.

где М = e + ïАï

Теорема доказана.

Бесконечно малые функции.

Определение. Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если .

Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Пример. Функция f(x) = xⁿ является бесконечно малой при х®0 и не является бесконечно малой при х®1, т.к. .

Теорема. Для того, чтобы функция f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие

f(x) = A + a(x),

где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а).

Свойства бесконечно малых функций:

1) Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

2) Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а.

4) Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Используя понятие бесконечно малых функций, приведем доказательство некоторых теорем о пределах, приведенных выше.

Доказательство теоремы 2. Представим f(x) = A + a(x), g(x) = B + b(x), где

, тогда

f(x) ± g(x) = (A + B) + a(x) + b(x)

A + B = const, a(х) + b(х) – бесконечно малая, значит

Теорема доказана.

Доказательство теоремы 3. Представим f(x) = A + a(x), g(x) = B + b(x), где

, тогда

A×B = const, a(х) и b(х) – бесконечно малые, значит

Теорема доказана.

Поиск по сайту: