 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Калькуляторные и решательные моделирующие комплексы
|
Читайте также: |
Большенство стандартных программных комплексов можно отнести к Мощным калькуляторам для статических вычислений и Специализиро-ванным решателям для моделирования динамических процессов.
Реализация калькуляторных и решательных программ предусматривает определение последовательности математических функций соответствующими вычислительными модулями. Однако в калькуляторных программах происходит однократное вычисление запланированной последовательности функций а в программах – решателях выполняется повторная последовательность вычислений в динамическом режиме работы технического устройства.
Каждая из программ математического моделирования динамических систем основана на одной из двух технологий:
1. Первая технология предполагает использование поточной модели управления при выполнении математических преобразований (функций) составляющих модель. Эти программы легко интегрируются с системами сбора данных, благодаря чему возможно создание (компьютерных) моделей с физическими объектами в контуре. В большинстве из них возможно программирование цифровых сигнальных процессоров. Структура их моделей может меняться согласно событийному управлению.
2. Вторая технология предполагает представление модели в виде текстовой записи системы уравнений, которую решатели моделирующих программ обрабатывают в пакетном режиме. Эти программы, в скрытом от пользователя режиме, преобразуют текстовую запись систем уравнений к требуемому решателям виду. В этом случае с пользователя снимается задача подключения к модели итерационного решателя алгебраических уравнений. Эти особенности технологии позволили не ограничиваться моделями в виде передаточных функций. Они предоставляют пользователю возможность строить модели в виде технологических схем.
Главным затруднением для разработчиков моделирующих программ является графический интерфейс, который, должен быть полноценным редактором векторной графики.
Явный решатель моделирующей программы -э то библиотека классических подпрограмм (функций), которые реализуют операцию интегрирования. (Дискретные квазианалоги интеграторов используются для решения дифференциальных уравнений).
Неявный (итерационный) решатель моделирующей программы -э то библиотека классических подпрограмм, которые предназначены для решения алгебраических уравнений путем итерационного подбора независимых переменных.
Оптимизирующий решатель моделирующей программы -э то разновидность неявного решателя, которая предназначена для минимизации значения функции в процессе итерационного подбора ее независимых переменных.
13. Обобщённая структура моделирующих комплексов
Архитектура программ математического моделирования
динамических систем имеет модульную структуру

Графический интерфейс отвечает за представление математической модели в виде, понятном широкому кругу специалистов. Это могут быть блок-схемы, схемы физические принципиальные, гибридные карты состояний и пр.
СУБД отвечает за хранение исходных, промежуточных и итоговых данных составленной пользователем модели и осуществляет управляемую трансформацию структуры хранилища данных.
Математическое ядро осуществляет основную вычислительную нагрузку, и в цикле, согласно заданной программе, обеспечивает исполнение потоков математических функций.
Подсистема визуализации обеспечивает интерфейс между функционирующим математическим ядром и пользователем.
14. Компонентные и топологические уравнения для моделирования методом эквивалентных схем.
Компонентные уравнения отражают законы функционирования элементов. Они формируются на основе знаний о конкретной предметной области. Связь между элементами осуществляется топологическими уравнениями.
Формы Компонентных и Топологических уравнений для объектов различной физической природы одинаковы.
В большинстве технических систем можно выделить три типа простейших элементов R, С, L. В первом элементе R происходит преобразование кинетической и потенциальной энергии в тепловую. Элементы С и L накапливают потенциальную или кинетическую энергию. Сочетанием этих элементов и источников сигналов получаем ММ любой сложности. Таким образом, существующие аналогии между переменными параметрами в системах различной физической природы сведены в таблицу:
| Природа системы | Фазовые переменные | Компоненты | |||
| поток | потенциал | типа R | типа C | типа L | |
| Электри- ческая | Ток | Напряжение | Электр.сопр. | Электр емкость | Электрическая индуктивность |
| Механ. поступа- тельная | Сила перемещения | Скорость перемещения | Механическое трение перемещения | Механ. масса элемента | Механическая упругость пружины |
| Механ- враща- тельная | Момент вращ. | Угловая скорость | Механ. трен. вращения | Механ момент вращения | Механическая вращательная гибкость |
| Гидравл. (пневм) | Расход жидкости (газа) | Давление жидкости (газа) | Гидравл(пневм) сопрот. | Гидравл (пневматическая) емкость | Гидравл (пневмат индуктивность |
| Теплотехническая | Поток | Температ. | Тепловое сопротивл. | Тепловая емкость |
15. Уравнения электрических систем
Фазовыми переменными электрических систем являются I и U
Компонентные уравнения имеют следующий вид:
1.Уравнение сопротивления  , где
, где  - электрическое сопротивление.
- электрическое сопротивление.
2.Уравнение емкости  , где
, где  - электрическая емкость.
- электрическая емкость.
3.Уравнение индуктивности  , где
, где  -электрическая индуктивность.
-электрическая индуктивность.
Топологические уравнения имеют вид:
1. Уравнение первого закона Кирхгофа  , где
, где  - ток
- ток  -й ветви
-й ветви
2. Уравнение второго закона Кирхгофа  , где
, где  - падение напряжения на
- падение напряжения на  -й ветви, входящей в контур.
-й ветви, входящей в контур.
16. Уравнения механических поступательных систем
Фазовые переменные:  - сила
- сила  - скорость
- скорость
Компонентные уравнения:
1. Уравнение вязкого трения  , где
, где  - механическое сопротивление перемещению (величина обратная коэффициенту вязкого трения)
- механическое сопротивление перемещению (величина обратная коэффициенту вязкого трения)
2. Уравнение массы (уравнение 2 закона Ньютона 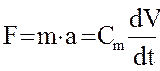 ,
,
где  - ускорение,
- ускорение,  - масса элемента
- масса элемента
3. Уравнение пружины  , где
, где  - упругость пружины.
- упругость пружины.
Топологические уравнения:
1. Уравнение Даламбера для поступательных систем: 
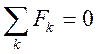 ,
,
где  - сила, приложенная к телу
- сила, приложенная к телу
2. Уравнение сложения скоростей на участке перемещения  , где
, где 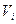 - абсолютная, относительная или переносная скорость.
- абсолютная, относительная или переносная скорость.
17. Уравнения механических вращательных систем.
Фазовыми переменными являются моменты силы М и угловые скорости ω. Компонентные уравнения имеют следующий вид:
1. уравнение вязкого трения вращения  , где
, где 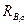 -механическое сопротивление вращению (величина, обратная коэффициенту трения вращения);
-механическое сопротивление вращению (величина, обратная коэффициенту трения вращения);
2. уравнение динамики вращательного движения  , где
, где  -момент инерции элемента;
-момент инерции элемента;
3. уравнение кручения бруса 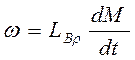 , где
, где  - вращательная гибкость;
- вращательная гибкость; 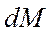 - момент кручения.
- момент кручения.
Топологические уравнения:
1. уравнение Даламбера для вращательных систем  , где
, где  - момент силы (включая момент инерции) действующей относительно оси вращения.
- момент силы (включая момент инерции) действующей относительно оси вращения.
2.Уравнение принципа сложения угловых скоростей вдоль оси вращения
 , где
, где 
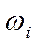 - угловая скорость.
- угловая скорость.
18. Уравнение гидравлических (пневматических) систем
Фазовые переменные гидравлических систем - объемные расходы G и давление Р. Запишем уравнения трех типов простейших элементов:
1) уравнение для участка трубопровода при стационарном течении жидкости:
G=P/Rг,  где Rг - гидравлическое сопротивление;
где Rг - гидравлическое сопротивление;
τ-кинетическая вязкость; l - длина трубопровода; d-диаметр трубопровода.
2) уравнение сжимаемости жидкости в объеме при воздействии давления: G=Сг(dP/dt), Сг=K·τ где Сг - гидравлическая емкость; К-коэффициент объемной сжимаемости; τ-кинетическая вязкость;
3) закон движения идеальной жидкости Р=Lг(dG/dt), Lг= l /s где Lг - гидравлическая индуктивность; s-площадь поперечного сечения трубопровода; l - длина трубопровода.
Топологические уравнения гидравлических (пневматических) систем
Записывается следующим образом:
1) уравнение равновесия потоков: ∑ Gк=0, где Gк - поток, втекающий в узел или вытекающий из него;
2) уравнение непрерывности давлений:: ∑ Pi=0, где Pi-падение давления в ветви, входящей в контур.
Пневматические системы аналогичны гидравлическим.
19. Уравнения теплотехнических систем
Фазовые переменные этой системы - тепловые потоки Ф и температура Т. Запишем уравнения трех типов простейших элементов:
1) уравнение теплообмена: Ф=Т/Rт, где Rт тепловое сопротивление, зависящее от площади поперечного сечения и длины рассматриваемого участка;
2) уравнение теплоемкости тела: Ф=Gт (dT/dt), где Gт - удельная теплоемкость тела;
3) в том случае, когда фазовыми переменными являются тепловой поток и температура, компонентное уравнение, соответствующее тепловой индуктивности, не имеет физического смысла.
Топологические уравнения данных систем имеют следующий вид:
1) уравнение равновесия тепловых потоков в узлах системы:
∑ Фк=0, где Фк - тепловой поток, втекающий в узел или вытекающий из него;
2) уравнение непрерывности тепловой системы: ∑ Tι =0, где Tι - разность температур на участке, входящем в контур.
20. Эквивалентные схемы механических поступательных систем
При построении ММ механической поступательной системы в эквивалентной схеме выделяют элементы, массу которых необходимо учесть. Такие элементы изображаются двухполюсниками массы. Первый полюс таких двухполюсников соединяется с базовым узлом, отражающим инерциальную систему отсчета. Второй представляет собой саму массу (через него осуществляется все взаимодействия элемента с окружающей средой). Далее выделяются элементы трения и упругости. Элемент трения включается между контактируемыми телами, элемент упругости- между телами, соединенными упругой связью. Внешние усилия, прикладываемые к механической системе, отображаются источниками силы (типа потока) и узлами, к которым подключены элементы массы, подвергающиеся усилию.
Пример механической поступательной системы (горизонтальное движ. автом)


F-тяга автомоб; М1 – масса автомоб: М2 - масса груза в кузове; М3 - масса прицепа; М4 - масса погруженного груза в прицеп. TRS1 и TRS2 - трение между колёсами и дорогой; R1 и R2-трение скольжения грузов о поверхности автомобиля и прицепа; UP1-упругость сцепления автомобиля и прицепа; UP2, UP3-упругости тросов, удерживающих груз массой М4.
21. Эквивалентные схемы механических вращательных систем
В эквивалентных схемах механических вращательных систем базовый узел, соответствует неподвижной невращающейся части объекта. Ветвь, изображающая момент инерции, включается между базовым узлом, через который осуществляется взаимодействие тела с данным моментом инерции и телами, находящимися с ним на одной оси вращения.
Пример механической вращательной системы (муфта сцепления).


F1 - нагрузка на входном валу муфты; F2 - нагрузка на выходном валу муфты; TRS1 и TRS2-коэффициенты трения в подшипниках; UP1 и UP2-упругость кручения валов; С1 и С2-момент инерции ведущего и ведомого дисков муфты; TRV-переменный коэффициент трения между дисками сцепления.
22. Моделирование подвески колеса при его вертикальном перемещении


П-пружина V-источник скорости, определяемый профилем дороги
А-амортизатор UP1-упругость колеса m1-масса колеса
К-колесо m2-масса подвижной части амортизатора
UP2-упругость пружины TRS-трение в амортизаторе
Рычаг подвески отображен на ММ зависимыми источниками Fp и Ep, и представляет собой трансформатор сил и скоростей: Fp=k*FEp; Ep=k*VFp; k=L1/L2, здесь FEp-усилие (в ветви источника Ер), воздействующее на малое плечо рычага, VFp-скорость на большем конце рычага (вертикальная скорость колеса); L1 и L2 –соответствующие плечи рычага.
23. Моделирование редуктора






Углы эквивалентной схемы соответствуют угловым скоростям, а ветви-моментам сил. ММ редуктора состоит из вращательных частей, взаимодействие между которыми осуществляется зубчатыми трансформатором моментов. Зацепления представлены зависимыми источниками момента и угловой скорости М1V1 (первое зацепление), М2V2 (второе зацепление).
Для первого зацепления М1=k1·МV1, V1=k1·VМ1 где k1=D2/D1-передаточное отношение. D1 и D2-диаметры зубчатых колес с моментами инерции С1 и С2. МV1-момент на элементе V1, противодействующий вращению первого колеса со стороны второго; VM1-источник угловой скорости для 1-го колеса со стороны 2-го.
Для второго зацепления М2=К2·МV2; V2=К2·VM2; где К2=D4/D3,
где К2-перед-е отнош-е; D3 и D4 –диам-ры зубч-х колес с моментами инерции С3 и С4.
Мвх-момент на входе редуктора; Мн-момент нагрузки; Up4, Up8-крутильные гибкости зубчатых колес; Up1, Up2, Up3, Up5, Up6, Up7, Up9-крутильные гибкости валов;R1…R4-коэфф-ты трения в подшип-ках с учетом приведенного трения в зубчатых зацеплениях.
24. Моделирование гидравлических (пневматических) систем
В ММ гидро (пневмо) систем за базовый узел принимается внешняя среда. Резервуары моделируются гидроемкостями, которые одним полюсом подключаются к базовому узлу, а другим осуществляется взаимодействие этой гидроемкости с трубопроводами и другими гидроэлементами.






Трубопроводы на эквивалентной схеме отображены гидравлическими сопротивлениями R1-R2 и гидроиндуктивностями L1-L2. Источник давления Р1 отражает тот факт, что давление на соответствующем выходе из С3 меньше на величину Р1, чем у дна емкости: Р1= ρ·q·h, ρ - плотность жидкости; q - ускорение свободного падения; h - высота, на которой установлен трубопровод с дросселем D4.
25. Моделирование трансформаторной связи методом эквивалентных схем

Механическая вращательно-поступательная система. Мn- момент источник, создаваемого электродвигателем с моментами инерции С1, R1 и R2-трение в подшипниках, UP-вращательная упругость вала, С2-момент инерции блока, m и TRS-масса и трение поступательной системы. Источники V и F представляют трансформаторную связь между поступательной и вращательной подсистемами.
26. Моделирование гираторной связи методом эквивалентных схем.


Гидроцилиндр совокупность гидравлической и механической систем. Гидравлическая система на эквивалентной схеме представлена источником давления Р который через трубопровод (элементы R1 и L1) нагнетает жидкость в переменную емкость С1. Механическая подсистема представлена источником усилия F2, который, преодолевая трение штока TRS1 о стенки, через упругость штока UP передвигает поршень массой m1,имеющий трение TRS2 о стенки цилиндра.
Воздействие на гидравлическую подсистему со стороны механической учитывается источником расхода G, который зависит от скорости движения поршня, т. е. G = K1* V при K1 = S, где S- площадь поперечного сечения поршня; V- скорость движения поршня. Источник силы F1 учитывает воздействие гидравлической подсистемы на механическую. F1 = K2 * P при K2 = S, где P- давление в ёмкости C1.
27. Моделирование автономной системы водоснабжения. 
1. Водозаборный трубопровод.
2. Насос для подачи воды в сборный резервуар.
3.Сборный резервуар.
4.Насос для подачи воды по трубопроводу.
5.Гидролиния.
6.Напорная регулирующая ёмкость.
7. Трубопровод к потребителю.
При моделировании АСВ сделаем ряд допущений.
1. Вода источника артезианская, поэтому потребность в очистных сооружениях отпадает
2. В разводящей сети имеется одна точка отбора.

На схеме:

Rг1, Lг1 – Rг8, Lг8 – модели трубопроводов
Esn1,2 – источники синусоидального напряжения дизель – генераторов.
TRA1,2 – трансформ связь электр части дизель генераторов и их вращающихся частей.
TRS1,8 – коэффициенты трения в подшипниках дизель – генераторов.
UP1,5 – крутильные гибкости ведомых валов дизельных – генераторов.
C1,6 – моменты инерции ведомых валов дизельных – генераторов.
TRS2,9 – коэффициенты трения муфт ведомых валов генераторов и входных валов двигателей.
Mвх1,2 – моменты на ведущих валах двигателей.
TRS3.10 – коэффициенты трения в подшипниках ведущих валов.
UP2,6 – крутильные гибкости ведущих валов двигателей.
C2,7 - моменты инерции ведущих валов двигателей.
C3,8 - моменты инерции ведомых валов двигателей.
UP3,7- крутильные гибкости ведомых валов.
Mвых1,2 – моменты на выходе валов.
TRS4,11 - коэффициенты трения первых зубчатых и червячных зацеплений.
C4,9 – моменты инерции первых зубчатых и червячных зацеплений.
Mω1,2 – моменты противодействия вращению первых зубчатых колёс со стороны вторых.
TRS5,12 - коэффициенты трения вторых зубчатых и червячных зацеплений.
C5,10 - моменты инерции вторых зубчатых и червячных зацеплений.
P1,2,3,4,5,6,7– источники давления.
Cг1,2 – гидроёмкости цилиндров насосов.
GIR1,2 – гираторные связи.
M1,2 – массы поршней.
TRS6,13 – трение поршней о стенки цилиндров.
UP4,8 – упругости истоков поршней.
TRS7,14 – трение штоков о пазы цилиндров.
F1,2 – усилия действующие на штоки насосов.
G1,2 – источники расхода жидкости.
CR1,R2 – ёмкости сборного и регулирующего резервуаров.
28. Моделирование электрической сигнализации с тепловыми извещателями методом эквивалентных схем.
Тепловые извещатели реагируют не на факт повышения температуры,
а на скорость её повышения.

1. Модель электромагнитного реле; 2. Модель теплового извещателя.
Где:
Uоп. – напряжение основного источника питания
М1 – масса электромагнита с катушкой реле
М2 – масса ферромагнитного якоря реле
М3 – масса золотника клапана реле
UP1 – пружина для настройки хода якоря и золотника реле
R1- переключающий контакт
Lл1, Rл1 – модель сигнальной лампы
M4 – масса плавкой вставки извещателя
M5 – масса штольневой трубки извещателя
M6 – масса резьбовой крышки извещателя
M7 – масса штока упирающегося во вставку извещателя
TRS1 – трение при перемещении штока
UP2 – пружина для замыкания контакта R2 извещателя
R2 – переключающийся контакт извещателя
R3 – шунтирующий резистор
L1 – L3 – катушки лучевых реле
М8 – М10 – массы элементов дымозасасывающих трубок
Lл2, Rл2 – модель звена световой сигнализации
29. Моделирование систем методом искусственного интеллекта
Повышение интеллектуальности подсистем моделирования и проектирования осуществляется путем использования эвристического программирования экспертных систем, путем перехода от режима диалога к пакетному режиму.
Существует несколько проблем искусственного интеллекта возникающих на этапах моделирования и проектирования.
1. Представление знаний — разработка методов и приемов для формализации и последующего ввода в память интеллектуальной системы знаний из различных проблемных областей, обобщение и классификация накопленных знаний, применение знаний при решении задач.
2. Моделирование рассуждений — изучение и формализация различных схем человеческих умозаключений, используемых в процессе решения разнообразных задач, создание эффективных программ для реализации этих схем в вычислительных машинах.
3. Диалоговые процедуры общения на естественном языке, обеспечивающие контакт между интеллектуальной системой и человеком-специалистом в процессе решения задач.
4. Планирование целесообразной деятельности — разработка методов построения программ сложной деятельности на основании тех знаний о проблемной области, которые хранятся в интеллектуальной системе.
5. Обучение интеллектуальных систем в процессе их деятельности, создание комплекса средств для накопления и обобщения умений и навыков, накапливаемых в таких системах.
Искусственный интеллект реализует два направления:
 |
30. Основы моделирования процессов методом кле́точного автома́та
Клеточный автомат это дискретная модель которая включает регулярную решётку ячеек, каждая из которых может находится в одном из конечного множества состояний, таких как 0 и 1. Решетка может быть любой размерности. Для каждой ячейки определено множество ячеек, называемых соседством. Для работы клеточного автомата требуется задание начального состояния всех ячеек, и правил перехода ячеек из одного состояния в другое. На каждой итерации, используя правила перехода и состояния соседних ячеек, определяется новое состояние каждой ячейки. Обычно правила перехода одинаковы для всех ячеек и применяются сразу ко всей решётке.
Основное направление исследования клеточных автоматов — алгоритмическая разрешимость тех или иных проблем. Также рассматриваются вопросы построения начальных состояний, при которых клеточный автомат будет решать заданную задачу.
Модели на основе клеточных автоматов представляют собой одну из ветвей имитационного моделирования. Они представляют собой алгоритм функционирования системы, который не имеет аналога в виде математической модели, так что динамика изменения состояния такого автомата может быть исследована только путем модельного эксперимента, и заранее предсказать закономерности его развития невозможно.
Модельным клеточным автоматом называется сеть из дискретных клеток, меняющих свое состояние в дискретные моменты времени. Чаще всего рассматриваются двумерные клеточные автоматы, элементами которых являются квадратные клетки (впрочем, форма клеток может быть и иной — треугольник, шестиугольник и т. д.). Каждая клетка может находиться в одном из конечного числа состояний, а время в данной модели представлено дискретным множеством тактов. Состояние каждой клетки автомата в последующий момент времени определяется ее собственным состоянием и состоянием ближайших соседей в предыдущий момент. Среда предполагается однородной, т. е. правила изменения состояний для всех клеток одинаковы. Если эти правила зависят от случайных факторов, то автомат называется стохастическим; в противном случае — детерминированным.
С помощью клеточных автоматов целесообразно моделировать такие сложные процессы, как самоорганизация технических систем, морфогенез, турбулентность и даже социальные процессы. Результаты моделирования на основе клеточных автоматов имеют простую наглядную графическую форму отображения.
31. Моделирование сложных технических систем
Сложными системами считаются крупные технологические, производственные, энергетические, коммуникационные комплексы, системы управления, социальные, экономические, экологические системы и т. п., которые могут быть искусственного или естественного происхождения.
Сложные системы характеризуются большим количеством элементов и связей, разнообразием взаимодействий между системой и окружающей средой, наличием случайных факторов внутренней и внешней природы, возможностью случайного изменения структуры.
Обычно выделяют структурную и поведенческую сложность моделируемых объектов.
Для систем сложного поведения характерно несколько качественно различных, последовательно сменяющих друг друга во времени режимов функционирования. Подобная сложная динамическая система в каждый конкретный момент времени ведет себя как некоторая относительно простая динамическая система, однако при определенных условиях режим ее функционирования скачкообразно меняется. Например, гидротехническое сооружение с двумя трубами обладает сложным поведением, поскольку его поведение при переполнении качественно отличается от его поведения при нормальном уровне воды или при опорожнении.
К основным функциям сложных систем относятся:
1. Модели сложных систем помогают упорядочить представления
о свойствах этих систем. В технике такие модели служат в качестве
средства для создания новых, более совершенных систем.
2. Модели сложных систем применяются как средство для обучения лиц, которые должны уметь справляться со всевозможными случайностями до возникновения критической ситуации (модели космических кораблей, тренажеры для обучения водителей, операторов АЭС и др.).
3. Одним из важных применений моделей сложных систем является прогнозирование поведения моделируемых объектов и диагностика их состояния.
4. Модели сложных систем позволяют производить контролируемые эксперименты в ситуациях, когда экспериментирование на реальных объектах экономически нецелесообразно, опасно или практически невозможно.
Естественно, что при исследовании сложной системы, содержащей большое количество элементов, невозможно детально моделировать процессы в каждом элементе. С общесистемной точки зрения представляют интерес только те свойства элементов, которые непосредственно влияют на свойства системы в целом.
Модельное исследование сложных динамических систем выполняется на основе пакетов визуального моделирования, которые позволяют вводить описание моделируемой системы в естественной для прикладных наук форме. Имеется возможность рисовать функциональную схему, размещать на ней блоки различного рода факторов, в том числе случайных, и прослеживать их влияние. Детальные компьютерные эксперименты с моделью системы позволяют лучше понять законы ее функционирования и разработать предложения по ее улучшению, которые были бы невозможны без имитации.
Имитация сложных систем дает представление о наиболее существенных факторах, определяющих ее свойства, позволяет исследовать новые ситуации, которые ранее были неизвестны, и провести предварительную проверку различных стратегий принятия решений перед проведением экспериментов на реальной системе, позволяет экспериментально исследовать сложные внутренние взаимодействия в системе, будь то отрасль, отдельная фирма или экономика в целом.
32. Моделирование стохастических процессов.
Моделирование случайных (стохастических) процессов — это одно из важнейших направлений имитационного моделирования. Событие называется случайным, если оно достоверно непредсказуемо..
В практике моделирования это экономические, социальные, экологические, производственные и любые другие системы, в которых значительную роль играет человеческий фактор.
В задаче оптимального размещения ресурсов предполагается, что для всех ее параметров известны точные значения, или, иными словами, все параметры такой задачи считаются детерминированными. Однако на практике точных значений этих параметров просто не существует. Действительно, при выполнении любой работы могут быть непредсказуемые перебои с поставками сырья; цены на рынке подвержены колебаниям и т. п. Все эти факторы имеют случайный характер, и говорить об их конкретных значениях можно только с определенной вероятностью.
При моделировании случайных процессов значительно изменяется сама методология моделирования. Основными методами изучения подобных систем становятся стохастическое моделирование и статистическая обработка его результатов.
Стохастическое моделирование — это метод получения с помощью компьютера статистических данных о процессах, происходящих в моделируемой системе, параметры которой изменяются случайным образом с заданным законом распределения. Сущность метода стохастического моделирования сводится к построению моделирующего алгоритма, имитирующего функционирование системы, случайные воздействия на систему, случайные изменения параметров системы и случайные изменения начальных условий. Такой алгоритм многократно реализуется с помощью компьютерных программных средств, в результате чего получается серия частных значений искомых величин, статистическая обработка которых позволяет получить информацию о свойствах системы. Если количество таких реализаций велико, то полученные результаты с достаточной точностью могут характеризовать процесс функционирования системы. В ходе модельных экспериментов с помощью имитационной модели воспроизводится влияние случайных факторов. При этом, для получения статистических данных о свойствах объекта или про-цесса требуется его многократное воспроизведение в ходе моделирования.
Подобный метод был разработан и применяется для решения детерминированных аналитических задач, получив название метода Монте-Карло. Согласно ему детерминированная вычислительная задача заменяется эквивалентной схемой некоторой стохастической системы, выходные характеристики которой совпадают с результатом решения этой задачи.
33. Моделирование виртуальных приборов средствами LabVIEW
LabVIEW – среда разработки прикладных программ, использующая специфический язык графического программирования и не требующей написания текстов программ.
Среда программирования, LabVIEW имеет библиотеки функций и подпрограмм для приема данных, их анализа и обработки. Реализации программ LabVIEW называются виртуальными инструментами, поскольку их внешнее графическое представление и способ функционирования имитируют работу реальных физических приборов. Виртуальные инструменты имеют интерактивный интерфейс пользователя, представленный в виде передней панели, аналогичной панели реального физического прибора и содержащей ручки управления, кнопки, графические индикаторы и другие средства управления и индикации. Источником кода виртуального инструмента служит блок-схема, отображающая графическое представление программируемой задачи.
Программная реализация виртуальных инструментов использует в своей работе принципы иерархичности и модульности. Виртуальный инструмент, содержащийся в составе другого виртуального инструмента, называется прибором-подпрограммой. Данный комплекс способен моделировать сложные технические измерительные приборы.
34. Основы моделирования методом конечных элементов
| Метод конечных элементов (МКЭ) — численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной техники. Метод широко используется для решения задач механики деформируемого твёрдого тела (сопромата), теплообмена, гидродинамики и электродинамики. |
Суть метода следует из его названия. Область, в которой ищется решение, разбивается на конечное количество подобластей (элементов). В каждом из элементов произвольно выбирается вид функции. Вне своего элемента функция равна нулю. Значения функций на границах элементов (узлах) является решением задачи и заранее неизвестно. Коэффициенты функций обычно ищутся из условия равенства значения соседних функций на границах между элементами (в узлах). Затем эти коэффициенты выражаются через значения функций в узлах элементов. Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов. Так как каждый из элементов связан с ограниченным количеством соседних, система линейных алгебраических уравнений имеет разряжённый вид, что существенно упрощает её решение.
С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей информационного дерева — путём его расчленения.
Наиболее полно метод реализуется в моделирующем комплексе ELCUT. Он проволяет моделировать электромагнитные, тепловые и механических процесссы:
– Линейная и нелинейная магнитостатика.
– Магнитное поле переменных токов (с учетом вихревых токов).
– Нестационарное магнитное поле.
– Электростатика.
– Электрическое поле переменных токов в неидеальном диэлектрике.
– Растекание токов в проводящей среде.
– Линейная и нелинейная, стационарная и нестационарная теплопередача.
– Линейный анализ напряженно-деформированного состояния.
– Связанные задачи.
35. Ф ункциональное моделирование систем.
Функциональное моделирование применяется для анализа функциональных схем при их проектировании. Процедура проектирования последних соответствует общей схеме функционального блока. Целью их анализа является проверка правильности функционирования системы на данном этапе ее разработки.
Математические модели функциональных схем должны быть более простыми, чем полные математические модели, получаемые методами схемотехнического проектирования. Для технических агрегатов используются два подхода к синтезу математической модели функциональных схем.
Первый подход основан на макромоделировании. Модели элементов в этом случае соответствуют упрощенным эквивалентным схемам этих элементов. Объединение моделей элементов в общую модель схемотехнического устройства выполняется с помощью метода переменных состояний или узлового метода. Математическая модель устройства представляет собой систему дифференциальных уравнений, а фигурирующие в ней фазовые переменные. Трудности такого подхода заключаются в том, что отсутствуют формализованные методики получения технических макромоделей, а также в сравнительно большой размерности получаемых систем уравнений.
Второй подход базируется на использовании функционального моделирования, развитого в теории математического управления. Макромодели элементов систем в этом случае представляются в виде передаточных функций. Данная модель элемента уже не техническая, она не отображает связи между фазовыми переменными. Здесь в каждом узле схемы, в отличие от технических, используется только одна фазовая переменная, являющаяся носителем информации, которая называется сигналом.
Объединение моделей элементов в модель системы осуществляется на основе отождествления входных и выходных сигналов, соответствую-щих соединяемым входам и выходам элементов.
Поиск по сайту: