 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Схема взаимосвязи технологических этапов моделирования

6. Моделирование и принятие решений в условиях неопределенности
Воздействие на технические объекты осуществляется на основе принятых осознанных решений. Процесс появления решений проходит три основных стадии:
 |
Информационно-аналитическая подготовка состоит из:
1.Постановки задачи
2.Поиска, накопления и предварительной обработки информации для ПР;
3.Выявление и оценка текущей ситуации с учетом возникшей проблемы;
4. Выдвижение гипотез, вариантов, альтернатив и сценариев;
Решение представляет собой главный системообразующий результат, который вырабатывается в процессе ПР и реализуется в рамках некоторой системы принятия решений (СПР).
 |
7. Классы аналитических задач принятия решения
Объект воздействия, для аналитических задач СПР может быть формально описан следующими параметрами:
1. Пространство состояний объектов; 2. Множество характеристик, признаков, описывающих состояние объекта управления и принимающих свои значения в любом множестве; 3.Пространство управления (решений, проектов, планов и.д.); 4.Время (дискретное или непрерывное); 5. Пространство выходных значений (наблюдаемых проявлений и оценок); 6. Отображение динамики изменения состояния объекта, реакции динамической системы на управляющие воздействия;
7. Выходное отображение, описывающее процесс наблюдения объекта управления (получение оценок, мнений); 8. Внешние неуправляемые факторы, оказывающие влияние на динамику объекта управления.
Для любого технического объекта аналитические задачи, необходимые для принятия решений, могут быть разбиты на три основных класса аналитических задач.

8. Математические подходы, модели и теории для решения задач в условиях неопределённости
Для решения аналитических задач в СПР, возникающих в процессе моделиро-вания систем управления сложными объектами, используются различные подходы.

9. Основные виды неопределенности на этапах моделирования
 |



На сегодняшний день можно выделить ряд математических теорий предназначенных для формализации неопределенной информации (данных):
1. Многозначная логика;
2. Теория вероятности;
3. Теория ошибок;
4. Теория средних интервалов;
5. Теория субъективных вероятностей;
6. Теория нечетких множеств;
7.Теория нечетких мер и интегралов.
Результаты сравнения математических теорий, с точки зрения их
применимости для решения аналитических моделирующих задач СПР в условиях неопределенности.
| № | Учитываемая характеристика | Подходы к учету факторов неопределенности | ||||||
| Учет физической числовой неопределенности | - | + | + | + | + | + | + | |
| Учет физической нечисловой неопредел-ости | + | - | - | + | + | + | + | |
| Учет нечисловой лингвистической неопр-ти | + | - | - | - | + | + | + | |
| Зависимость ошибки конечного результата от точности задания исходных данных | + | - | - | - | + | + | + | |
| Возм-ость учета семантической модальности | + | - | - | - | - | - | + | |
| Возможность количественной оценки неопр. | - | + | - | - | + | + | + | |
| Учет квалификации | - | + | - | - | + | + | + | |
| Возможность учета противоречия между точностью и неопределенностью | + | - | - | + | + | + | + | |
| Эффективность формализации всей исходной информации | + | - | + | + | + | + | + | |
| Отсутствие требования жесткого задания полного перечня событий | + | - | + | + | - | + | + | |
| Возможность эффективного учета взаимо- влияния неопределенности при обработке | + | - | - | - | - | - | + | |
| Возможность одновременного получения Пессимистических и оптимистических оценок и уровня доверия к ним | - | + | - | + | + | + | + | |
| Единый подход к представлению точных, неопределенных, неполных, нечетких значений атрибутов | - | - | - | - | - | - | + | |
| Возможность реализации алгоритмов обработки информации | + | + | + | + | + | + | + | |
| Возможность работы на профессиональном языке пользователя | + | - | - | - | - | + | + | |
| Простота выявления экспертных знаний | + | - | + | + | - | + | + | |
| Возможность работы с неопрдел. информацией, основанной на малых статистич. выборках | + | - | + | + | - | + | + | |
| Наглядность получаемых результатов расчета для оценки рисков | - | - | - | - | - | + | + |
10. Моделирование методом планирования эксперимента
После создания математической модели и её программной реализации важным этапом является постановка вычислительного эксперимента. В теории планирования эксперимента исследуемый объект рассматривается как черный ящик, имеющий входы X и выходы Y.

Переменные Х называются факторами, которые в эксперименте могут быть – качественными и количественными. Качественным факторам присваиваются числовые обозначения, тем самым осуществляется переход к количественным значениям. Переменные Х можно геометрически сопоставить с факторным пространством, координатные оси которого соответствуют значениям факторов. Совокупность значений факторов во всех точках плана эксперимента образует матрицу плана ПФЭ для n=4:
| № выч. | Х 1 | Х 2 | Х 3 | Х 4 | Р |
| + | + | + | + | 
| |
| - | + | + | + | 
| |
| + | - | + | + | 
| |
| - | - | + | + | 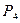
| |
| + | + | - | + | 
| |
| - | + | - | + | 
| |
| + | - | - | + | 
| |
| - | - | - | + | 
| |
| + | + | + | - | 
| |
| - | + | + | - | 
| |
| + | - | + | - | 
| |
| - | - | + | - | 
| |
| + | + | - | - | 
| |
| - | + | - | - | 
| |
| + | - | - | - | 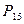
| |
| - | - | - | - | 
|
Обрабатывая вектор результатов Р методом наименьших квадратов определяем вектор коэффициентов модели 
Модель в общем виде для четырех факторов на двух уровнях имеет вид
 Полученные коэффициенты будут характеризовать вес каждого фактора
Полученные коэффициенты будут характеризовать вес каждого фактора
11. Возможности основных комплексов математического моделирования динамических систем
Весь процесс математического моделирования невозможен без математических вычислений. Поэтому, математическое ядро каждого моделирующего динамические процессы комплекса имеет ряд возможностей для выполнения различных математических вычислений.
Поиск по сайту: