АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Дисциплина «Математика». Преподаватель, доцент Каневская И.Ю._____________

Читайте также:
  1. II. Дисциплинарные производства в отношении сотрудников правоохранительной службы
  2. Автономия, дисциплина и просоциальное поведение
  3. Адаптивное физическое воспитание как наука и учебная дисциплина
  4. АКАДЕМИЧЕСКАЯ ДИСЦИПЛИНА
  5. Взаимодействие со смежными дисциплинами.
  6. Включение психологии в состав многих междисциплинарных исследований.
  7. Воинская дисциплина, ее сущность и значение
  8. Вторая стадия производства - рассмотрение дела о дисциплинарном проступке и принятие по делу решения.
  9. Глава 1. МУНИЦИПАЛЬНОЕ ПРАВО КАК ОТРАСЛЬ РОССИЙСКОГО ПРАВА, НАУКА И УЧЕБНАЯ ДИСЦИПЛИНА
  10. Глава 1. Политология как наука и учебная дисциплина ... 4
  11. Глава 7. ДИСЦИПЛИНАРНЫЕ МЕРЫ: ЗАМЕЧАНИЯ, ПРЕДУПРЕЖДЕНИЯ, ДИСКВАЛИФИКАЦИИ
  12. Гносеология как философская дисциплина. Сущность и структура познавательной деятельности.

Шифр_______________

Группа___________________________________________________

Ф.И.О.____________________________________________________________

Подпись студента_____________

Преподаватель, доцент Каневская И.Ю._____________

Вариант №5

Вопрос 1. Бесконечно малые и бесконечно большие величины и связь между ними.

Вопрос 2. Дифференциал функции.

Вопрос 3. Неопределенный интеграл и его свойства.

Вопрос 4. Найти пределы: а) ; б) .

Вопрос 5. Найти производную функции: а)

1. б)

Вопрос 6. Найти частные производные функции: z= 8x2 – xy + 2y2 – 16x + y – 1.

 

Дисциплина «Математика»

Шифр_______________

Группа___________________________________________________

Ф.И.О.____________________________________________________________

Подпись студента_____________

Преподаватель, доцент Каневская И.Ю._____________

Вариант №6

Вопрос 1. Функция двух переменных и её график.

Вопрос 2. Теорема об инвариантности формы первого дифференциала сложной функции.

Вопрос 3. Производная сложной функции.

Вопрос 4. Найти пределы: а) 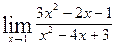; б) .

Вопрос 5. Найти производную функции: а)

1. б)

Вопрос 6. Найти частные производные функции: z= 3 – 2x2 – xy – y2.

 
1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)