 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнение Д. Бернулли для струйки невязкой жидкости
При установившемся движении локальные ускорения равны нулю, т. е.
,
и уравнения Эйлера (4.2) записываются в виде:
(4.22)
Умножим первое из уравнений (4.22) на dx:
. (4.23)
Преобразуем правую часть (4.23) с учетом того, что 
:
.
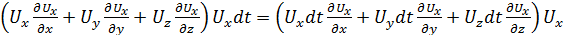Но Uxdt, Uydt и Uzdt - проекции на оси Ox, Oy и Oz перемещения частицы жидкости вдоль элементарной струйки, т. е. соответственно равны dx, dy и dz, поэтому исследуемое выражение можно представить в виде
,
где dUx - полный дифференциал компоненты Ux скорости частицы, определяемой вдоль элементарной струйки.
Так как 
, то уравнение (4.23) запишем в виде
.
Аналогично преобразуем второе и третье уравнения системы (4.22):
.
Сложим полученные уравнения и сгруппируем слагаемые в них:
. (А)
Положим, что объемные силы, действующие на жидкость, обладают потенциалом, то есть существует такая скалярная функция Π, для которой
; 
; 
.
Тогда
Xdx+Ydy+Zdz=dΠ.
При установившемся движении
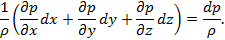
Наконец,
.
Следовательно, вместо (А) можно написать
. (4.24)
Проинтегрируем (4.24) вдоль линии тока:
(4.25)
Это уравнение пригодно и для трубки тока, если скорости во всех точках сечения одинаковы и зависят только от S. Постоянная в правой части неизменна вдоль одной линии тока и изменяется при переходе к другой линии.
Если движение происходит только под действием силы тяжести, то силовая функция П=-gz и уравнение (4.25) записывается в виде
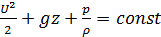, (4.26)
или, после деления на g,
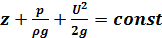. (4.27)
Выражение (4.27) - уравнение Бернулли для струйки установившегося движения идеальной несжимаемой жидкости.
Иногда уравнение (4.27) называют законом Бернулли, поскольку оно представляет следствие закона сохранения энергии для стационарного потока идеальной несжимаемой жидкости.
Здесь z - геометрическая высота центра тяжести сечения струйки над горизонтальной плоскостью x0y; p/ρg - пьезометрическая высота; U 2/2 g - скоростная высота.
Литература по содержанию лекции:
1. Чугаев Р. Р. Гидравлика (Техническая механика жидкости). - Л.: Энергоиздат, 1982. - 672 с.
2. Штеренлихт Д. В. Гидравлика. - М.: Энергоатомиздат, 1985. - 640 с.
Поиск по сайту: