ТЕСТИРОВАНИЕ ГСЧ

1. Определение периода случайных чисел:

· задается какое-либо случайное число;

· если не известен алгоритм формирования случайных чисел и нет гарантии того, что начальное число ставит генератор в его собственный цикл, то необходимо произвести генерацию последовательности достаточно большого количества чисел, например, 2000 и запомнить последнее число;

· производят сравнение с этим запомненным числом каждого последующего числа, поступающее с выхода ГСЧ и считают их количество;

· при совпадении очередного числа с запомненным определяется его номер, который и является периодом генерируемой последовательности.

2. Проверка равномерности распределения случайных чисел:

· интервал (0, 1) разбивается на М равных подынтервалов (рекомендуется брать М=20);

· генерируется достаточно большое количество случайных чисел Z (рекомендуемое количество по 20 на один подынтервал), например, N=400, каждое из которых попадает в один из подынтервалов;

· определяют количество чисел N_m, которые попали в m-й подынтервал;

· определяют относительную частоту (оценку вероятности) Р_m попадания случайных чисел из общей последовательности в каждый из подынтервалов Р_m = N_m/N;

· определяют оценку плотности вероятности

р = P_mM и строят гистограмму и интегральную эмпирическую функцию распределения чисел;

· оценивают степень соответствия экспериментально полученных зависимостей теоретическим используя критерии согласия (Колмогорова, Пирсона и др.)

(См. Е.С. Венцель «Теория вероятности»)

3. Проверка стохастичности случайных чисел:

· задают различные вероятности события р;

· формируют потоки единиц по алгоритму В(n) = ent[R(n) + p];

· задают различную длину потоков чисел N;

· оценивают на каждой заданной длине потока чисел N распределение вероятности числа j единиц: P^*(j, N)= ;

· в различных взятых вариантах задания р и N результат оценки распределения вероятности Р^* сравнивают с теоретическими расчетами Р по формуле Бернулли (биномиальным распределением):

P(j, N) = ;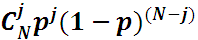

· проверяют соответствие оценок распределения вероятности Р^* и теоретического значения распределения вероятности Р по известным критериям согласия.

4. Проверка независимости случайных чисел осуществляется посредством измерения автокорреляционной функции:

· берут последовательность случайных чисел {R(n)};

· задерживают на число N эту последовательность с помощью дискретной линии задержки: {R(n-N)};

· округляют случайные числа R(n) до значений R^*(n) с точностью до ±Δr<<1;

· определяют оценку корреляционного момента (ковариации) последовательности округленных случайных чисел:

K_N = ,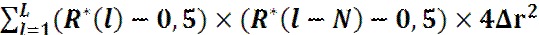

где 2Δr – это вероятность того, что равномерно распределенное на интервале от 0 до 1 случайное число попадает в интервал ±Δr;

· оценку корреляционного момента последовательности случайных чисел определяют для различных значений задержки N;

· числа считаются независимыми, если оценка корреляционного момента K_N для разных N незначительно отличается от нуля при достаточно больших значениях L.

Поиск по сайту: