Плоское движение

Плоское движение - это такое движение твердого тела, при котором траектории всех его точек лежат в параллельных плоскостях. Если в теле провести некоторую прямую O₁O₂, перпендикулярную этим плоскостям (рис. 1.9), то все точки этой прямой будут двигаться по одинаковым траекториям с одинаковыми скоростями и ускорениями; сама прямая будет, естественно, сохранять свою ориентацию в пространстве. Таким образом, при плоском, или, как его иногда называют, плоско-параллельном, движении твердого тела достаточно рассмотреть движение одного из сечений тела

бсолютно твердым телом называют тело, деформациями которого в условиях данной задачи можно пренебречь. Когда же твердое тело будет оставаться в покое? Твердое тело будет оставаться в покое, если нет причин, вызывающих его движение. Для этого необходимо и достаточно выполнение двух условий:

1. .

(25.1)

результирующая всех внешних сил, приложенных к телу, должна быть равной нулю.

2. .

(25.2)

суммарный момент всех внешних сил относительно любой точки должен быть равен нулю.

Эти условия должны быть выполнены в той системе отсчета, относительно которой тело покоится.

Плоским движением называется такое движение, при котором все точки тела движутся в параллельных плоскостях.

Произвольное плоское движение можно представить как совокупность поступательного движения и вращения.

Рис.25.1. Произвольное плоское движение твердого тела.

Пусть цилиндр радиуса R катится без скольжения по плоскости. Рассмотрим движение точек: А, В, С, их линейные скорости: V_A, V_B, V_C. Скорость поступательного движения - V₀. За начало координат примем одну из точек, лежащих на оси вращения, а линейная скорость вращательного движения равна:

,

тогда:

.

(25.3)

скорость точек тела относительно неподвижной системы отсчета.

Особенно удобным оказывается разбиение произвольного плоского движения на поступательное, происходящее со скоростью движения центра масс - V_C и вращения вокруг оси, проходящей через этот центр: [w, r]. Например, для точки В имеем:

.

(25.4)

или

.

(25.5)

ассмотрим твердое тело. Разобьем его на множество элементарных масс, и представим его как систему частиц с неизменными расстояниями между ними. Тогда:

,

(26.1)

где Dm_i - i-элементарная масса; r_i-радиус-вектор, определяющий положение i-й массы. Но формула (26.1.) не дает вполне однозначное значение, т.к. каждый из r_i можно проводить в любую точку элементарной массы. Эту неоднозначность можно устранить, если Dm_i®0. Тогда:

,

(26.2)

В формуле (26.2.) интегрирование ведется по всему объему тела. Введем понятие плотности тела для характеристики распределения массы по объему тела. Однородным будем называть тело, свойства которого во всех точках одинаковы, тогда:

,

(26.3)

где m-масса тела; V-его объем.

Если тело неоднородно, то плотность в точке Р:

,

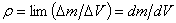(26.4)

DV®0

где Dm-масса заключенная в объеме DV, а точка Р находится внутри объема DV. DV-физически бесконечно малый объем, т.е. объем, внутри которого свойства вещества в его пределах можно считать одинакоыми, но он достаточно велик, чтобы не могла проявиться дискретность вещества. Из (26.4.) следует: dm=rdV и

.

(26.5)

Твердое тело эквивалентно системе частиц (материальных точек), тогда:

Центр масс твердого тела движется так, как двигалась бы частица (материальная точка) с массой, равной массе тела, под действием всех приложенных к нему сил

.

(26.6)

Уравнение моментов в векторной форме для движения центра масс твердого тела имеет вид:

Поиск по сайту: