АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Реактивное движение

Читайте также:
  1. Антигоспитальное в области психиатрии движение в мире во второй половине XX века
  2. Билет 26. Движение декабристов.
  3. Быстрое выдвижение
  4. В первой четверти XIX в. Движение декабристов.
  5. Взаимное движение капиталов
  6. Военно-фашистское движение и милитаризация страны. Путч 15 мая 1932 г.
  7. Вопрос 4: Траектория движения. Криволинейное движение. Нормальное и тангенциальное ускорения при криволинейном движении.
  8. Вопрос№5 Движение по окружности. Связь угловой и линейной скорости
  9. Вращательное движение и его кинематические параметры. Связь между угловой и линейной скоростями.
  10. Вращательное движение твердого тела
  11. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
  12. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА

Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.

Реактивное движение – это движение, возникающее при отделении от тела с некоторой скоростью какой-либо его части. Яркий пример реактивного движения – надутый воздухом воздушный шарик, который, если его развязать, приходит в движение.

Рассмотрим другой яркий пример. При стрельбе из орудия возникает отдача – снаряд движется вперед, а орудие – откатывается назад. Снаряд и орудие – два взаимодействующих тела. Скорость, которую приобретает орудие при отдаче, зависит только от скорости снаряда и отношения масс (рис. 1.17.2). Если скорости орудия и снаряда обозначить через и 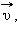а их массы через M и m, то на основании закона сохранения импульса можно записать в проекциях на ось OX

 

Рисунок 1.17.2. Отдача при выстреле из орудия

На принципе отдачи основано реактивное движение. В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью относительно ракеты. Обозначим массу выброшенных газов через m, а массу ракеты после истечения газов через M. Тогда для замкнутой системы «ракета + газы» на основании закона сохранения импульса (по аналогии с задачей о выстреле из орудия) можно записать:

где V – скорость ракеты после истечения газов. В данном случае предполагается, что начальная скорость ракеты равнялась нулю.

Полученная формула для скорости ракеты справедлива лишь при условии, что вся масса сгоревшего топлива выбрасывается из ракеты одновременно. На самом деле истечение происходит постепенно в течение всего времени ускоренного движения ракеты. Каждая последующая порция газа выбрасывается из ракеты, которая уже приобрела некоторую скорость.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)