АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Существование функции ценности

Читайте также:
  1. D. Субъективный характер меры ценности. Труд и ценность. Заблуждение
  2. F. Метод, основанный на использовании свойства монотонности показательной функции .
  3. I Психологические принципы, задачи и функции социальной работы
  4. I. Деньги и их функции.
  5. I. Функции
  6. I. Функции эндоплазматической сети.
  7. I.1.8. Философия и ценности.
  8. II. Основные задачи и функции
  9. II. Основные задачи и функции
  10. II. Функции плазмолеммы
  11. II.4.3.Три драгоценности буддизма
  12. III. Предмет, метод и функции философии.

 

Рассмотрим случай существования функции ценности. Пусть 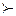– некоторое асимметричное и транзитивное отношение строгого предпочтения на множестве оценок Y Rm.

Определение: Числовую функцию Ф переменных у 1, у 2, …, уm называют функцией ценности для отношения 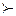, если для произвольных векторов y, y' Î Y неравенство Ф (у)> Ф (у') имеет место тогда и только тогда, когда 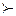у у'.

 

Предположим, что отношение 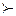удовлетворяет аксиоме Парето. Поэтому если у 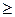у', то у 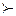у', следовательно, Ф (у)> Ф (у'). Поэтомуфункция ценности (если она существует) является возрастающей по отношению ≥.

Если Ф (у) – функция ценности для отношения 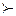и h – возрастающая функция одной переменной, то h [ Ф (у)]также является функцией ценности. То есть функция ценности определяется с точностью до возрастающего преобразования h, в частности функция αФ (у) +a, где α >0 и a Î R является функцией ценности, если Ф – функция ценности.

По определению неразличимости ~, отношение у~у' выполняется тогда и только тогда, когда не верно ни соотношение у 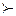у', ни соотношение у' 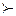у. Поэтому, если Ф (у) =Ф (у'), то не может быть ни Ф (у)> Ф (у'),ни Ф (у')> Ф (у), а значит верно соотношение у~у'. Верно и обратное, то есть из у ~ у' следует Ф (у) =Ф (у').

Используя функцию ценности, вопрос сравнения по предпочтительности векторных оценок у и у' можно свести к сравнению соответствующих чисел Ф (у)и Ф (у').

Если для отношения 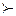существует функция ценности Ф, то 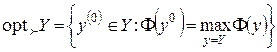, то есть отыскание оптимальной оценки сводится к решению однокритериальной задачи максимизации функции Ф на множестве Y.

Необходимым условием существования функции ценности является транзитивность отношения ~ (неразличимости). Это следует из определения функции ценности и транзитивности отношения равенства =.

Отношение 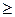на Rm порождает нетранзитивное отношение неразличимости, поэтому для отношения 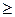на Rm функции ценности не существует. Однако, в частных случаях, например, если множество Y конечно и имеет вид:

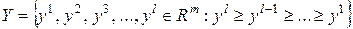, функция ценности существует, например, 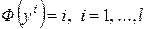. Следовательно, существование функции ценности зависит и от структуры множества Y.

Вопрос о построении функции ценности можно найти в книге П. Фишберна "Теория полезности для принятия решений" (М.: Наука, 1976).

 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)