Выбор решения при строго упорядоченных по важности критериях

Часто для ЛПР желательно получить как можно большее значение, например, критерия f ₁, даже за счет «потерь» по остальным критериям, то есть критерий f ₁ оказывается более важным, чем остальные. Возможен и случай, когда весь набор критериев f ₁, f ₂,..., f_m строго упорядочен по важности.

Пусть имеется два вектора .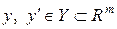

Определение: Лексико-графическое отношение определяется следующим образом: отношение имеет место тогда и только тогда, когда выполнено одно из следующих условий:

1) y ₁> y ₁ ' (71)

2) y ₁= y ₁ ', y ₂> y ₂^/

…………………

m) ; 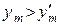, где .

Изменение нумерации критериев приводит к другому лексико-графическому отношению.

При m= 1 лексико-графическое отношение совпадает с отношением > на подмножестве вещественных чисел.

Если , то говорят, что вектор y лексико-графически больше, чем вектор y'.

Геометрическая иллюстрация отношения приведена на рисунке 1.

◦

Рисунок 1 – Геометрическая иллюстрация лексико-графического отношения

Если ЛПР в качестве отношения строгого предпочтения использует лексико-графическое отношение, то это означает, что из пары оценок для него предпочтительнее та, первая компонента которой больше (независимо от соотношений между остальными компонентами). Если первые компоненты двух оценок одинаковы, то для ЛПР предпочтительнее оценка, имеющая большую вторую компоненту; остальные компоненты данной оценки могут при этом «значительно уступать» соответствующим компонентам второй оценки и так далее. В таких случаях говорят, что компоненты у ₁, у ₂,..., у_m (то есть критерии f ₁, f ₂,..., f_m) строго упорядочены по важности.

Изменение нумерации критериев приводит к другому лексико-графическому отношению.

Теорема. Отношение асимметрично, транзитивно и удовлетворяет аксиоме Парето.

Доказательство. Покажем транзитивность лексико-графического отношения.

Пусть и , причём для первого соотношения справедливо условие (71) с некоторым номером а для второго – условие (71) с некоторым номером .

Положим . Тогда для оценок y и y' выполнено условие из (71) с номером n. Следовательно, , транзитивность доказана.

Так как не может быть выполнено ни для какого y, то лексико-графическое отношение иррефлексивно. Произвольное транзитивное и иррефлексивное отношение всегда асимметрично. Следовательно, отношение асимметрично.

Если верно неравенство 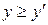, то одно из условий (71) будет выполнено. Поэтому из выполнения 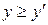, следовательно, , следовательно, лексико-графическое отношение удовлетворяет аксиоме Парето. ■

Пусть имеются векторы , следовательно, справедливо либо , либо . Если не выполнено ни одно из этих соотношений, то y=y'.

Лексико-графическое отношение на множестве оценок порождает отношение на множестве решений Х: тогда и только тогда, когда , где y=f (x), y'=f (x'). Очевидно, отношение также является асимметричным, транзитивным и удовлетворяет аксиоме Парето (в терминах решений).

Множество решений (оценок), оптимальных по отношению на множестве Х (соответственно Y), называется множеством лексико- графически оптимальных (или максимальных) решений (оценок) и обозначается (соответственно ).

Так как для любых двух векторов y, y' справедливо либо один лексико-графичекски больше другого, либо они равны, то множество , если оно не пусто, состоит из единственного элемента.

Следствие: Если множество Y состоит из конечного числа элементов, то лексико-графически оптимальная оценка существует и единственна.

Введем множества, определяемые рекуррентным способом:

– множество всех точек максимума первой компоненты вектор-функции f ₁ на множестве Х,

– множество всех точек максимума f ₂ – второй компонент вектор-функции f на множестве Х ₂,

…………………………………………

.

Имеют место включения .

Теорема. Для того чтобы решение было лексико-графически оптимальным, необходимо и достаточно, чтобы выполнялось включение .

Доказательство:

Необходимость.

Пусть . Предположим противное <=> либо .

В первом случае найдется такое решение , что и , что противоречит оптимальности 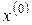. Поэтому выполняется , следовательно, и либо . Рассуждая аналогично, получаем и так далее. Окончательно получаем . Полученное противоречие доказывает необходимость.

Достаточность.

Рассмотрим решение 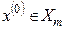и допустим противное: существует решение , для которого , следовательно, , где , . Пусть, согласно , выполняется k -условие из (33), . Тогда , а значит, в силу вложенности множеств имеем . Противоречие. ■

Следствие: Если все функции непрерывны на непустом компактном множестве 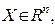то справедливо 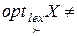Ø.

Доказательство:

По теореме Вейерштрасса (если множество не пусто и компактно, а функция f непрерывна на нём, то множество точек глобального минимума (максимума) не пусто и компактно) множество X ₁ не пусто и компактно. Тогда таким же свойством обладает и множество X ₂ и так далее до X_{m -1}. Множество Х_m не пусто в силу того, что X_{m -1} не пусто и компактно, а функция f_m – непрерывна. Следовательно, по предыдущей теореме множество лексико-графически оптимальных решений также не пусто. ■

Доказанная теорема даёт следующий поэтапный метод нахождения лексико-графически оптимального решения. Сначала находят множество точек максимума функции f ₁ на Х, то есть Х ₁. Далее на этом множестве максимизируют функцию f ₂и определяют множество X ₂ и так далее до множества X_{m -1}. Наконец, максимизируя f_m на X_{m -1}, находят лексико-графически оптимальное решение.

С точки зрения вычислений этот метод сложен, так как на каждом k - этапе (кроме последнего) нужно целиком строить множество Х_k. Удобнее для нахождения лексико-графически оптимального решения решать такую последовательность задач:

1) найти 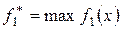при условии ;

2) найти при условиях , ;

………………………………..

m-1) найти при условиях , ;

m) найти точку максимума функции при условиях , .

1.3 Оценка сверху для множества оптимальных решений в условиях отношения предпочтения, инвариантного относительно перенумерации критериев

Лексико-графическое отношение не является инвариантным относительно перенумерации критериев. Однако на практике встречаются задачи, в которых для ЛПР не важно, в каком порядке перечисляются компоненты у ₁, у ₂, ..., у_m оценки y Î R^m, а важны только числовые значения этих компонент.

Пусть имеется вектор . Множество векторов, которое состоит из у и всех векторов, получившихся из у перестановкой его компонент, обозначим через П (у). Это множество содержит m! элементов. Элементы множества П (у) обозначим .

Считаем, что отношение строгого предпочтения 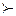определено на множестве , оно асимметрично, транзитивно и удовлетворяет аксиоме Парето.

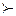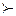Отношение называется инвариантным относительно перенумерации критериев, если из соотношения у у' следует , .

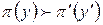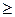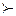Например, отношение на пространстве R^m не является инвариантным относительно перенумерации критериев: . Если для отношения существует функция ценности вида , то это отношение инвариантно относительно перенумерации критериев.

Будем считать, что отношение строгого предпочтения 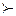инвариантно относительно перенумерации критериев.

Введем понятие симметрического отношения.

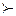Говорят, что на множестве задано симметрическое отношение , если соотношение у у' выполняется тогда и только тогда, когда для некоторого верно неравенство .

Например, для m =2, точка у, для которой , принадлежит объединению двух заштрихованных углов, расположенных симметрично относительно биссектрисы координатного угла (рисунок 2).

Рисунок 2 – Геометрическая интерпретация симметрического отношения.

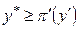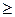
Симметрическое отношение транзитивно и асимметрично. Действительно, пусть , у^* у' => , для , . Переставим компоненты вектора у^* так, чтобы получился вектор . Аналогично переставим компоненты , чтобы получился . Тогда , то есть . Транзитивность установлена.

Симметрическое отношение иррефлексивно. Действительно, из выполнения следует , то есть сумма компонента вектора у больше суммы компонента вектора , а этого не может быть. Из транзитивности и иррефлексивности следует асимметричность.

Симметрическое отношение инвариантно относительно перенумерации критериев и удовлетворяет аксиоме Парето, то есть из следует .

Теорема. Справедливы соотношения:

, (72)

где – множество оптимальных оценок по отношению на множестве Y;

– множество парето-оптимальных оценок на множестве .

Доказательство:

Проверим включение из соотношения (72). Пусть . Предположим противное: для некоторого 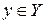для некоторой перестановки . Отсюда, согласно аксиоме Парето, следует, что . Используя инвариантность отношения 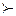относительно перенумерации критериев, получаем . Это противоречит . Таким образом, .

Теперь докажем . Пусть .

Предположим противное: 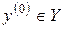и 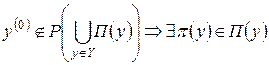такое, что 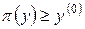. Переставляя компоненты векторов, входящих в это неравенство, получим , где . Противоречие. Справедливость обратного включения доказывается аналогично. ■

Таким образом, множество оптимальных оценок по отношению является оценкой сверху для множества оптимальных оценок.

В этом случае, если одна из оценок предпочтительнее другой, то и каждая оценка, полученная из первой перестановкой компонент, является более предпочтительной, чем оценка, образованная из второй оценки произвольной перестановкой компонент. Используя эти сведения, можно сузить множество парето-оптимальных оценок.

2 Построение обобщенного критерия в многокритериальной задаче принятия решений

Оценка сложных систем в условиях определенности на основе методов векторной оптимизации проводится в три этапа:

- на первом этапе определяются частные показатели и критерии эффективности;

- на втором этапе находится множество Парето и задача многокритериальной оптимизации формулируется как задача отыскания множества оптимальных оценок;

- на третьем этапе задача решается путем скаляризации критериев и устранения многокритериальности.

В методах свертывания векторного критерия в скалярный первоначальная задача заменяется задачей:

y*(x) —> extr,

где y*(x) - скалярный критерий, представляющий собой некоторую функцию от значений компонентов векторного критерия:

y*(x) = f (y1(x), y2(x), y3(x),..., ym(x)).

Основной проблемой этого подхода и является пост­роение функции f, называемой сверткой. Данная проблема рас­падается на четыре задачи:

1. Обоснование допустимости свертки.

2. Нормализация критериев для их сопоставления.

3. Учет приоритетов (важности) критериев.

4. Построение функции свертки, позволяющей решить задачу оптимизации.

1. Обоснование допустимости свертки. Требует подтвержде­ния, что рассматриваемые показатели эффективности являются однородными. Известно, что показатели эффективности разде­ляются на три группы: показатели результативности, ресурсоем­кости и оперативности. В общем случае разрешается свертка по­казателей, входящих в обобщенный показатель для каждой груп­пы отдельно. Свертка показателей из разных групп может привести к потере физического смысла такого критерия.

2. Нормализация критериев. Проводится подобно нормиров­ке показателей, которая осуществляется, как правило, введением относительных безразмерных показателей, представляющих собой отношение «натурального» частного показателя к некоторой нормирующей величине, измеряемой в тех же единицах, что и сам показатель

y_{i норм} =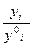

где в знаменателе – некоторое «идеальное» значение i-го показателя.

Выбор нормирующего делителя для перевода частных показателей в безразмерную форму в значительной мере носит субъективный характер и должен обосновываться в каждом конкретном случае.

Возможны несколько подходов к выбору нормирующего делителя:

1) нормирующий делитель y_i⁰ можно задавать с помощью ЛПР, и это предполагает, что его значение является образцовым;

2) можно принять, что нормирующий делитель y_i⁰ = max y_{i j};

3) в качестве нормирующего делителя может быть выбрана разность между максимальным и минимальным значениями показателя для перевода его в диапазон [0, 1].

3. Учет приоритетов критериев. Осуществляется в большин­стве методов свертывания путем задания вектора коэффициен­тов важности критериев

l = (l₁,l₂, …, l_m), ål_i =1,

где l_i - коэффициент важности критерия yi, обычно совпадающий с коэф­фициентом значимости частного показателя качества.

Определение коэффициентов важности критериев, как и в слу­чае с показателями, сталкивается с серьезными трудностями и сводится либо к использованию формальных процедур, либо к применению экспертных оценок.

В результате нормализации и учета приоритетов критериев вместо исходной векторной оценки y(x) альтернативы x образу­ется новая векторная оценка

y*(x) = (l₁y₁(x),l₂y₂(x), …, l_my_m(x))

y_i (x) – нормированный критерий.

Именно эта полученная векторная оценка подлежит преоб­разованию с использованием функции свертки. Способ свертки зависит от характера показателей и целей оценивания системы. Известны несколько видов свертки. Наиболее часто используют­ся аддитивная и мультипликативная свертка компонентов век­торного критерия.

Поиск по сайту: