 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
III этап: Анализ решения задачи
В результате решения задачи в рабочей книги появится новый лист Отчет по устойчивости (только при выборе пункта Устойчивость в диалоговом окне Результат поиска решения), который необходим для проведении анализа полученного решения.
Грамотно проанализировать решение задачи – одна из главных задач менеджера!
Данные на листе организованны в виде двух таблиц: Изменяемые ячейки и Ограничения (см. рис. 10).

рис. 10 Отчет по устойчивости
Таблица 3
Раздел Изменяемые ячейки
| Столбец | Значение | Комментарии и примеры |
| Ячейка | Адреса ячеек с неизвестными | |
| Имя | Имена неизвестных | |
| Результирующее значение | Оптимальные значения неизвестных, полученные в ходе решения задачи. | Равенство нулю переменных х2, х3, х4 означает, что данная продукция является убыточной, т.е. стоимость ресурсов, затраченных на производство одного изделия, больше чем цена продукта. |
| Нормированная стоимость | Если продукт входит в оптимальный план, в столбце Нормированная стоимость для этого продукта стоит 0. Если продукт не входит в оптимальный план, то в этом столбце стоит отрицательное число, абсолютная величина которого показывает на сколько нужно увеличить прибыль от продажи единицы этого продукта, чтобы он вошел в оптимальный план. | Пример:
Продукция второго вида не вошла в оптимальный план. Если увеличить прибыль от продажи продукции на 17 ед., т.е. она составит 25+17=42 ед., то станет выгодно выпускать изделия второго вида и оптимальное решение будет следующим
 = (0, 8,57, 0, 0), = (0, 8,57, 0, 0),
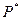 =360 руб.
Аналогичные расчеты можно проделать для 3 – его и 4 – ого продукта. =360 руб.
Аналогичные расчеты можно проделать для 3 – его и 4 – ого продукта.
|
| Целевой коэффициент | Коэффициенты, стоящие при неизвестных в целевой функции. | В данной задаче – прибыль от продажи 1-ой единицы каждого вида продукции. |
| Допустимое увеличение Допустимое уменьшение | Числа, показывающие, на сколько максимально можно увеличить или уменьшить прибыль от реализации единицы продукции данного вида при сохранении оптимального плана выпуска. Оптимальное значение ЦФ при этом может изменится. | Примечание: Число 1Е+30 (10 +30 - максимально известное компьютеру число) означает, что прибыль можно уменьшать (увеличивать) практически не ограниченно, но при этом оптимальное решение останется прежним.
Анализ полученных значений:
Т.о. получены следующие интервалы устойчивости:
продукция 1 вида – (30+ 1Е+30, 30- 12,142),
продукция 2 вида –
(25+ 17, 25- 1Е+30),
продукция 3 вида –
(8+ 16, 8- 1Е+30),
продукция 4 вида –
(16+ 32, 16- 1Е+30).
Пример:
Для продукции четвертого вида допустимое увеличение 32, а допустимое уменьшение не ограниченно.
Если увеличить прибыль от реализации единицы продукции данного вида на 15, т.е. она составит 16+15=31 руб., при этом оптимальное решение задачи не изменился
 =(12, 0, 0, 0), =(12, 0, 0, 0), 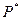 = 360 руб.
Аналогично, при снижении прибыли на 10 руб. оптимальное решение осталось прежним.
Если прибыль увеличить на 33 руб., т.е. она составит 16+33=49, то оптимальное решение изменится следующим образом: = 360 руб.
Аналогично, при снижении прибыли на 10 руб. оптимальное решение осталось прежним.
Если прибыль увеличить на 33 руб., т.е. она составит 16+33=49, то оптимальное решение изменится следующим образом:
 = (0, 0, 0, 7,5), = (0, 0, 0, 7,5), 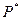 =367,5 руб. =367,5 руб.
|
Таблица 4
Раздел Ограничения
| Столбец | Примечание | Комментарии и примеры |
| Ячейка | Адреса ячеек с левыми частями ограничений | |
| Результирующее значение | Значения левых частей ограничений в результате решения задачи | |
| Теневая цена | Теневая цена показывает насколько изменится прибыть от производства всей продукции при увеличении правой части ограничения на 1 единицу (в рассматриваемой задачи – запаса данного ресурса на 1 единицу).
 + +  где
где  - теневая цена.
Теневая цена, также определяет ценность ресурса для производителя, если она отлична от 0, то ресурс считается дефицитным. - теневая цена.
Теневая цена, также определяет ценность ресурса для производителя, если она отлична от 0, то ресурс считается дефицитным.
| Пример:
В нашем случае дефицитным ресурсом является оборудование (т.к. его теневая цена отлична от нуля)  =3.
Также, исходя из ограничения (3), видно, что оборудование использовано на 100 % (левая часть ограничения равна правой), в то время как остальные ресурсы использованы не полностью (левая часть ограничения меньше правой).
Пример:
Если дефицитный ресурс оборудование увеличить на 1 ед., то оптимальная прибыль изменится и станет равной =3.
Также, исходя из ограничения (3), видно, что оборудование использовано на 100 % (левая часть ограничения равна правой), в то время как остальные ресурсы использованы не полностью (левая часть ограничения меньше правой).
Пример:
Если дефицитный ресурс оборудование увеличить на 1 ед., то оптимальная прибыль изменится и станет равной 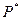 =360+3=363 руб. =360+3=363 руб.
|
| Ограничение правая часть | Значения правых частей ограничений | |
| Допустимое увеличение | Число, показывающие, на сколько можно увеличить запасы ресурса при сохранении его теневой цены.
При этом значение целевой функции изменится следующим образом:
 + +  ,
где ,
где  -величина увеличении ресурса, -величина увеличении ресурса,  - теневая цена. - теневая цена.
| Пример:
Если увеличить ресурс оборудование на  = 50 ед., то оптимальная прибыль составит = 50 ед., то оптимальная прибыль составит 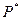 = =  =360+50*3=510 руб. =360+50*3=510 руб.
|
| Допустимое уменьшение | Число, показывающие, на сколько можно уменьшить запасы ресурса при сохранении его теневой цены.
При этом значение целевой функции изменится следующим образом:
 - -  ,
где ,
где  -величина увеличении ресурса, -величина увеличении ресурса,  - теневая цена. - теневая цена.
| Пример:
Если уменьшить ресурс оборудование на  = 100 ед., то оптимальная прибыль составит = 100 ед., то оптимальная прибыль составит
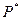 = =  =360-50*3=60 руб. =360-50*3=60 руб.
|
Примечание: Теневые цены и интервал устойчивости изменения запасов каждого из ресурсов, в котором значения теневых цен сохраняются, помогает менеджеру, не решая задачи заново, оценить, запасы какого ресурса нужно увеличить, чтобы максимально увеличить прибыль, и какого будет увеличение прибыли при заданном изменении данного запаса.
Поиск по сайту: