АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

I. 1.2. Общая постановка задачи линейного программирования

Читайте также:
  1. Data Mining и Business Intelligence. Многомерные представления Data Mining. Data Mining: общая классификация. Функциональные возможности Data Mining.
  2. I Психологические принципы, задачи и функции социальной работы
  3. I. 1.1. Пример разработки модели задачи технического контроля
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.1. Двойственная задача линейного программирования
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  8. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  9. I. Общая установка сознания
  10. I. Общая характеристика.
  11. I. Ситуационные задачи и тестовые задания.

 

Задача, в которой требуется обратить в максимум (минимум) целевую функцию

при условиях

(I. 1.1.)

 

называется общей задачей линейного программирования в произвольной форме.

Вектор 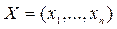, удовлетворяющий ограничениям задачи линейного программирования, называется ее решением или планом. Если при этом переменные еще и неотрицательны, то план является допустимым. Множество всех допустимых планов, образуют область допустимых решений (ОДР) задачи ЛП. Это выпуклое[5] многогранное множество. Поэтому задачи ЛП являются частным случаем более общих задач выпуклого программирования.

Допустимый план, соответствующий крайней[6] точке ОДР, является опорным планом, либо допустимым базисным решением задачи ЛП.

Допустимый план, обращающий в максимум (минимум) целевую функцию, называется оптимальным планом задачи ЛП.

 

Теорема (ЛП): Пусть допустимое множество задачи ЛП является многогранником (в обобщенном смысле). Если целевая функция принимает максимальное (минимальное) значение в некоторой точке множества , то она (точка) является крайней точкой для . Если целевая функция принимает максимальное (минимальное) значение более, чем в одной точке, то она принимает это же значение и в любой их выпуклой комбинации: Здесь внутренняя точка отрезка ; 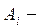граничная точка отрезка или крайняя точка ОДР; некоторый числовой параметр, «пробегающий» все значения из отрезка .

 


 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.89 сек.)