I.2.4. Алгоритм симплекс-метода

Шаг I: Выбор начального базисного решения.

Шаг II: Переход от начального решения к другому допустимому базисному решению с лучшим значением целевой функции (все решения, которые «хуже» исключаются).

Шаг III: Продолжение поиска допустимых базисных решений. (Если полученное решение не является оптимальным, то симплекс-метод позволяет перейти к смежному допустимому базисному решению).

Шаг IV: Смежное допустимое базисное решение отличается только одной базисной переменной (независимая переменная становится базисной, а одна из базисных переменных становится независимой). Тем самым осуществляется переход на соседнюю вершину многогранника ОДР.

Критерий оптимальности. Обозначим относительную оценку небазисной переменной 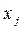через

оценки базисных переменных.

Если относительные оценки небазисных переменных допустимого базисного решения отрицательны или равны нулю, то соответствующее решение оптимально.

Проиллюстрируем все выше сказанное примером.

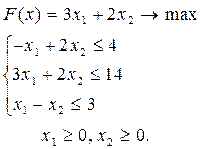
Приведем задачу к каноническому виду:

Здесь мы ввели в рассмотрение дополнительные переменные и , которые «уравновешивают» активные ограничения. Они же и образуют начальный базис.

Последовательные итерации удобно вести в компактном виде в таблице (см. таблицу I.).

Таблица I.

№ 1
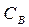
		-1
			-1

Элемент -максимальный из положительных в строке , следовательно – разрешающий столбец (он выделен). Таким образом, в базис необходимо ввести переменную . Далее, возникает вопрос о выводе из базиса одной из переменных. Ясно, что она выбирается далеко не произвольным образом. Для этого элементы столбца делим на соответствующие им по строке элементы разрешающего столбца и результат вписываем в рабочий столбец . При этом, отрицательный результат и результат деления на 0заменяем знаком . Отсюда, по компонентам столбца видно, что при увеличении (которая должна войти в базис) переменная будет оставаться положительной. Переменная станет равной 0 при . Однако, переменная станет равной 0быстрее, при . Это значение минимальное из компонент столбца . Таким образом, целесообразно сделать свободной, а базисной, тем самым осуществится переход на соседнюю вершину ОДР.

Далее элементарные гауссовы преобразования строк приведут исследователя к новому базису и новой таблице (таблица II).

Таблица II.

№ 2
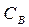
						-3
			-1
					-3

Сформулируем последовательность операций перехода к таблице II.

· Прибавить разрешающую строку к первой строке таблицы I. Результат записать в первую строку таблицы II.

· Умножить разрешающую строку на –3 и прибавить ко второй строке таблицы I. Результат записать во вторую строку таблицы II.

· Третья строка таблицы II – это разрешающая строка таблицы I, элементы которой разделены на разрешающий элемент (в клетке на пересечении разрешающей строки и разрешающего столбца).

· Строка так же вычисляется с помощью элементарных преобразований. По-прежнему, и это чрезвычайно важно, – рабочей строкой является разрешающая строка. Умножить третью строку таблицы I на –3 и прибавить к строке . Результат записать в строку таблицы II.

· Работа со строками таблиц осуществляется так, что последним (замыкающим строку) элементом является соответствующий элемент столбца .

· Вычислить значение целевой функции, как суммы произведений весовых коэффициентов, стоящих при базисных переменных на соответствующие элементы столбца .

Далее процесс продолжается до тех пор, пока не будет выполнен критерий оптимальности (см. таблицу III).

Таблица III.

№ 3
				-1

Таким образом,

Изобразим графически полученную ситуацию (см. рисунок I. 2.5).

Поиск по сайту: