I.2.3. Табличный симплекс-метод

Универсальным вычислительным методом решения задачи ЛП является так называемый симплекс-метод. Идея метода состоит в последовательном «улучшении» планов задачи по определенному критерию до получения оптимального решения.

Как уже было отмечено, оптимальное значение линейная целевая функция может достигать в крайних (граничных) точках ОДР, а именно в угловых точках. Важно заметить, что, если размерность задачи (количество переменных и количество ограничений) велики, то угловых точек может быть очень много и указать нужную становится весьма затруднительным делом, а определять оптимальное решение простым перебором весьма долгое и рутинное занятие.

Этих недостатков и лишен симплекс-метод, согласно которому: находясь в одной из вершин многогранной области – из всех соседних[8] вершин выбирается та, которая «улучшает» целевую функцию.

Рассмотрим процесс подготовки исходных данных и алгоритм решения задачи этим методом. Для решения задачи ЛП

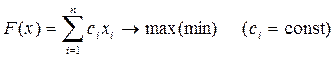
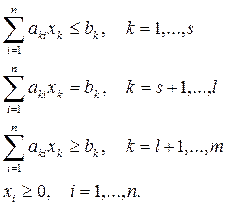
необходимо предварительно выполнить следующие процедуры:

- привести математическую модель задачи к каноническому виду (систему активных ограничений типа неравенств привести к уравнениям путем введения дополнительных «искусственных» переменных);

- определить начальное допустимое решение задачи;

- ввести в исходную таблицу параметры, соответствующие начальному опорному плану;

- весовые коэффициенты переменных целевой функции; переменные текущего базиса; значения базисных переменных (столбец ); элементы матрицы условий задачи (столбцы 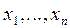); оценки «дефект» –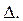

Оценки 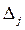определяются по формулам:

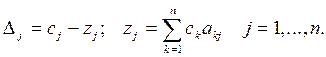
Весовые коэффициенты при базисных переменных проставляются в левый столбец таблицы. Значение целевой функции при текущем базисе

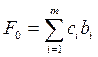
заносятся в последнюю строку столбца

Поиск по сайту: