 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
I.5.4. Решение задачи линейного программирования
После ввода исходных данных на экран выводится меню для выбора режима решения задачи (см. Фиг. 8). Режим решения определяет объем информации, выдаваемой на экран монитора в процессе решения задачи.
На Фиг. 9 показана начальная симплекс таблица задачи. В верхней части таблицы показаны имена переменных над соответствующими столбцами матрицы системы ограничений. Дополнительные и искусственные переменные вводятся автоматически и обозначаются: дополнительные – 
искусственные – 
Option Menu for Solving ggg
Меню режимов для решения <имя задачи>
When solving problem, you have the option to display steps of the simplex method.
При решении задачи Вы сможете выбрать режим просмотра шагов симплекс-метода.
This option is permissible only when your problem is small, that is, when
Этот режим возможен, только тогда, когда Ваша задача имеет небольшую размерность, то есть когда N+N1+N2+N3*2  9
N+N1+N2+N3*2  9, where N is the number of variables, N1 is the number of
где N - количество переменных, N1 - количество ограничений
“ ” constraints, N2 is the number of “=“ constraints, and N3 is the number
вида “ ”, N2 - количество ограничений вида строгих равенств (тождеств) и N3 - количество ограничений вида
of “  ” constraints; otherwise, only pivoting information will be displayed.
“  ”; иначе будет показана только краткая информация о каждой итерации.
| |
| Option Режим | |
| Solve and display the initial tableau Решить и показать начальную таблицу | |
| Solve and display the final tableau Решить и показать последнюю (конечную) таблицу | |
| Solve and display the initial and final tableau Решить и показать начальную и конечную таблицу | |
| Solve and display the every tableau Решить и показать каждую таблицу | |
| Solve without displaying any tableau Решить без показа таблиц | |
| Return to the functional menu Возврат в функциональное меню |
Передвигая курсор вверх или вниз выберите режим и нажмите ENTER.
Фиг. 8. Выбор режима решения задачи ЛП
В первом столбце приводятся имена базисных переменных, а во втором -коэффициенты целевой функции при базисных переменных. Видно, что столбцы матрицы при базисных переменных образуют единичную подматрицу (единичный, ортонормированный базис).
В предпоследнем столбце помещаются преобразованные свободные члены (при единичном базисе – просто свободные члены), которые при нулевых значениях свободных переменных равны значениям базисных переменных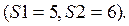 
В последнем столбце размещается отношение свободных членов к элементам выбранного (разрешающего) столбца. В начальной таблице выведены нулевые значения, так как разрешающий столбец еще не выбран. В первой таблице (см. Фиг.10) приведены реальные значения этих отношений.
В предпоследней строке таблицы выводятся относительные оценки всех переменных с отрицательными знаками, то есть 
а в последней строке - коэффициенты при “большом М”, если используется метод искусственного базиса.
Initial tableau
Начальная таблица
| 
| 
| 
| ||||
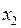
| Basis |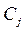 
| 1.000 | 2.000 | 0 | 
| 
| |
|
| 0 | 2.000 | 3.000 | 1.000 | 0.000 | 5.000 | 0 |
|
| 1.000 | 4.000 | 0.000 | 1.000 | 6.000 | 0 | |
| 1.000 | 2.000 | 0 | 0 | 0 | ||
| * Big M | 0 | 0 | 0 | 0 | 0 |
Нажмите любую клавишу для продолжения или “G” для
выхода на окончательное решение.
Фиг. 9-а. Начальная симплекс-таблица.
В текущей таблице более ярким цветом выделяются: относительная оценка переменной, выбранной для ввода в базис; минимальное отношение свободного члена к элементу выбранного столбца; переменная, выводимая из базиса и разрешающий элемент. Кроме того, на экран выводится номер итерации, текущее значение целевой функции, имя переменной, вводимой в базис и имя переменной, выводимой из базиса.
Конечная (финальная) таблица показана на Фиг. 11, где также приводится общее число итераций и оптимальное значение целевой функции.
Iteration 1
Итерация 1
|
|
|
|
| ||||
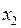
| Basis |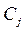
| 1.000 | 2.000 | 0 |
|
| |
|
| 0 | 2.000 | 3.000 | 1.000 | 0.000 | 5.000 | 1.667 |
|
| 1.000 | 4.000 | 0.000 | 1.000 | 6.000 | 1.500 | |
|
| 1.000 | 2.000 | 0 | 0 | 0 | ||
| * Big M | 0 | 0 | 0 | 0 | 0 |
Нажмите любую клавишу для продолжения или “G” для
выхода на окончательное решение.
Фиг. 9-б. Симплекс-таблица, соответствующая первой итерации
Current objective function value (Max.) = 0
| Текущая величина функции цели (Max) <Highlighted variable is the entering or leaving variable> <Повышенная яркость у переменных, входящих или выходящих из базиса> Entering: X2 Leaving: S2 Входящая Выходящая |
Нажмите любую клавишу для продолжения или “G”
для выхода на окончательное решение.
Фиг. 10. Текущая симплекс-таблица
(на примере первой итерации).
Final tableau (Total iteration =2)
Окончательная таблица (Всего итераций =2)
|
|
|
|
| ||||
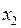
| Basis |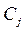
| 1.000 | 2.000 | 0 |
|
| |
|
| 1.000 | 1.000 | 0 | 0.800 | -0.600 | 0.400 | 0 |
|
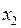
| 2.000 | 0 | 1.000 | -0.200 | 0.400 | 1.400 | 0 |
|
| 0 | 0 | -0.400 | -0.200 | 3.200 | ||
| * Big M | 0 | 0 | 0 | 0 | 0 |
(Max.) Optimal OBJ value = 3.2
(Max.) Оптимальная величина функции цели = 3.2
Нажмите любую клавишу для продолжения или “G”
для выхода на окончательное решение.
Фиг. 11. Окончательная симплекс-таблица.
Поиск по сайту: