 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Б). Дополнительная переменная – небазисная
|
Читайте также: |
Ограничение активно. Изменение свободного члена ограничений равносильно изменению дополнительной переменной, при котором происходит изменение всех базисных переменных. Некоторые из них могут уменьшаться, и, следовательно, достичь нулевого значения. Если  то из условия сохранения допустимости следует, что
то из условия сохранения допустимости следует, что

Если ограничение является неравенством типа “ 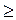 ”, то соответствующие диапазоны имеют следующие значения:
”, то соответствующие диапазоны имеют следующие значения:
· дополнительная переменная – базисная: 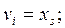
· дополнительная переменная – небазисная:

Если ограничение является равенством, то диапазона изменения свободного члена нет и любое его изменение приводит к необходимости преобразования базиса.
I.4.4.4. Диапазон изменения элемента матрицы коэффициентов системы ограничений
Рассмотрим изменение только элементов небазисных столбцов. Если  то изменится только относительная оценка небазисной переменной
то изменится только относительная оценка небазисной переменной  . Из условия сохранения оптимальности, то есть не отрицательности этой оценки:
. Из условия сохранения оптимальности, то есть не отрицательности этой оценки:
 если
если 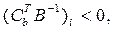
 если
если 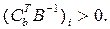
Поиск по сайту: