АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

II. 4.1. Алгоритм метода ветвей и границ

Читайте также:
  1. I.2.4. Алгоритм симплекс-метода.
  2. II. Проблема источника и метода познания.
  3. II. Типичные структуры и границы
  4. II.4. МЕТОД ВЕТВЕЙ И ГРАНИЦ В ЗАДАЧАХ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
  5. III Общий порядок перемещения товаров через таможенную границу Таможенного союза
  6. LU – алгоритм нахождения собственных значений для несимметричных задач
  7. QR- алгоритм нахождения собственных значений
  8. SALVATOR - это переход физического явления в семантико-нейронный алгоритм (инструкцию) освобождения человека от негативных последствий этого явления.
  9. SWOT-анализ в качестве универсального метода анализа.
  10. VII. СУЩЕСТВУЮТ ЛИ ГРАНИЦЫ ПОЗНАНИЯ?
  11. XII. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ

 

Рассмотрим частично целочисленную задачу вида:

 

 

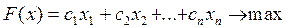
при ограничениях: целые для Здесь множество индексов целочисленных переменных.

 

Шаг I: решить сформулированную задачу как задачу ЛП, рассматривая все ее переменные как непрерывные. Отбрасывая условия целочисленности переменных, прийти к задаче ЛП I, оптимальное решение которой дает значение целевой функции: тогда считается верхней границей значений функции , если при этом какая-либо из переменных принимает дробное значение.

Шаг II: ветвление по одной из целочисленных переменных, имеющих дробное значение в оптимальном решении ЛП I.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)