АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

II.4. МЕТОД ВЕТВЕЙ И ГРАНИЦ В ЗАДАЧАХ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  4. I. 1.2. Общая постановка задачи линейного программирования
  5. I. 2.1. Графический метод решения задачи ЛП
  6. I. 3.1. Двойственная задача линейного программирования
  7. I. 3.2. Двойственный симплекс-метод.
  8. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  9. I. Метод рассмотрения остатков от деления.
  10. I. Методические основы
  11. I. Методические основы оценки эффективности инвестиционных проектов
  12. I. Организационно-методический раздел

Реализация этого метода заключается в последовательном ветвлении исходного множества решений на так называемое дерево подмножеств с нахождением решений на всех подмножествах, пока не будет получено искомое. По существу это некоторая процедура перебора всех целочисленных допустимых решений исходной задачи.

Для того чтобы изложение основных принципов метода ветвей и границ было достаточно иллюстративным, мы сразу параллельно изложению будем рассматривать конкретную числовую задачу.

 

 

Начальный шаг: решение задачи без учета условия целочисленности переменных.

 

Задачу

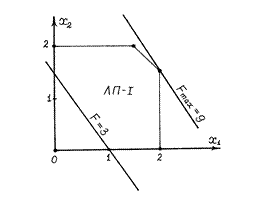
обозначим ЛП I. Она содержит всего лишь две переменные, поэтому ее можно решать, используя графический метод[15].

Из рисунка видно, что оптимальное решение задачи ЛП I достигается в точке , которой соответствует оптимальное решение при этом целевая функция достигает максимального значения

Поскольку принимает дробное значение, найденное решение не может быть оптимальным решением исходной задачи ЦЛП. Найденное значение представляет собой верхнюю границу истинного оптимального значения целевой функции задачи, поскольку при выполнении требований целочисленности значение может разве что уменьшиться[16].

 

Следующий шаг метода ветвей и границ состоит в просмотре целочисленных значений , больших или меньших . Это можно осуществить путем добавления к задаче ЛП I либо ограничения либо

 

Таким образом, из ЛП I получаются две задачи:

 

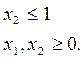
  ЛП II     при ограничениях:     новое ограничение:     ЛП III     при ограничениях:     новое ограничение:    

 

Допустимые области задач ЛП II и ЛП III обладают следующими свойствами:

10. Оптимальное решение ЛП I недопустимо для обеих ЛП II и ЛП III.

20. Любое целочисленное (допустимое) решение исходной задачи допустимо для обеих задач ЛП II и ЛП III.

Из решений ЛП II и ЛП III следует, что – это нижняя граница максимального значения целевой функции для исходной задачи ЦЛП.


 

       
   
 

 

    

Для ЛП III но план не является целочисленным, так как переменная принимает дробное значение. Поэтому необходимо проверить существование в

допустимой области задачи ЛП III целочисленного решения, дающего значение целевой функции . Для этого рассматриваются задачи ЛП IV и ЛП V, которые получаются в результате добавления к ЛП III дополнительных ограничений и 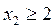соответственно.

 

Задача ЛП V допустимых решений не имеет, а допустимая область задачи ЛП IV – это отрезок (см. рисунок II.4.4.). Оптимальное решение ЛП IV даже визуально вполне очевидно: При этом значение целевой функции задачи Следовательно, для любого целочисленного решения в допустимой области ЛП III значение целевой функции не превосходит    

Таким образом, перебором установлено, что точка представляет собой оптимальное целочисленное решение исходной задачи.


 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (4.483 сек.)