 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Описание алгоритма решения Т-задачи
10. Предварительный этап:
Определяется начальный опорный план одним из указанных выше способов (например, методом северо-западного угла).
20. Первый шаг:
Вычисляется оценочная матрица  . Для расчета всех элементов матрицы необходимо сначала определить все потенциалы. Далее строится схема перевозок, соответствующая начальному опорному плану
. Для расчета всех элементов матрицы необходимо сначала определить все потенциалы. Далее строится схема перевозок, соответствующая начальному опорному плану  , то есть соединяем коммуникациями пункты отправления и пункты назначения, для которых
, то есть соединяем коммуникациями пункты отправления и пункты назначения, для которых  . Пользуясь выше указанными соотношениями для определения потенциалов по базисным клеткам, определяем последовательно все потенциалы пунктов отправления и назначения, принимая для удобства
. Пользуясь выше указанными соотношениями для определения потенциалов по базисным клеткам, определяем последовательно все потенциалы пунктов отправления и назначения, принимая для удобства  . Затем пересчитываем стоимости в небазисных клетках таблицы издержек. Очевидно, что позиции матрицы
. Затем пересчитываем стоимости в небазисных клетках таблицы издержек. Очевидно, что позиции матрицы  , отвечающие базисным элементам плана
, отвечающие базисным элементам плана  , будут заняты нулями.
, будут заняты нулями.
30. Итерации:
*  я итерация. Если в оценочной матрице
я итерация. Если в оценочной матрице 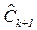 все элементы неотрицательны, то план
все элементы неотрицательны, то план  - оптимальный, в противном случае следует приступить к его улучшению;
- оптимальный, в противном случае следует приступить к его улучшению;
* выбирается наибольший по абсолютной величине отрицательный элемент оценочной матрицы  и, начиная с соответствующего ему элемента
и, начиная с соответствующего ему элемента  , в матрице
, в матрице  строится замкнутая цепочка[11], в которую входят элементы
строится замкнутая цепочка[11], в которую входят элементы  ;
;
* строится новый план  , прибавляя:
, прибавляя:  (минимальный элемент выбирается из только из тех элементов, которые связаны цепочкой) ко всем четным элементам цепочки и вычитая из нечетных[12]. Элементы матрицы
(минимальный элемент выбирается из только из тех элементов, которые связаны цепочкой) ко всем четным элементам цепочки и вычитая из нечетных[12]. Элементы матрицы  , не входящие в цепочку, переносятся в матрицу
, не входящие в цепочку, переносятся в матрицу  без изменения;
без изменения;
* далее с помощью эквивалентных преобразований (элементарные преобразования Гаусса) на основе матрицы  строится матрица
строится матрица 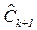 для нового плана
для нового плана  . Для этого необходимо выделить в матрице
. Для этого необходимо выделить в матрице  все элементы, соответствующие ненулевым элементам плана (они обязательно равны нулю). В матрице
все элементы, соответствующие ненулевым элементам плана (они обязательно равны нулю). В матрице  вычеркивается строка, содержащая элемент
вычеркивается строка, содержащая элемент  . Если в этой строке имеются выделенные элементы, то вычеркиваются соответствующие этим элементам столбцы. Если в каждом вычеркнутом столбце присутствуют выделенные элементы, то далее вычеркиваются им соответствующие строки и так далее, до тех пор пока описанная процедура выполнима. После этого ко всем элементам вычеркнутых строк прибавляется величина равная
. Если в этой строке имеются выделенные элементы, то вычеркиваются соответствующие этим элементам столбцы. Если в каждом вычеркнутом столбце присутствуют выделенные элементы, то далее вычеркиваются им соответствующие строки и так далее, до тех пор пока описанная процедура выполнима. После этого ко всем элементам вычеркнутых строк прибавляется величина равная  , а из элементов вычеркнутых столбцов эта величина вычитается. Таким образом получается новая оценочная матрица. Если в матрице
, а из элементов вычеркнутых столбцов эта величина вычитается. Таким образом получается новая оценочная матрица. Если в матрице 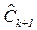 нет отрицательных элементов, то план на этом шаге оптимален. В противном случае необходимо выполнить еще одну итерацию.
нет отрицательных элементов, то план на этом шаге оптимален. В противном случае необходимо выполнить еще одну итерацию.
На этом итерации завершаются.
ПРИМЕР: Пусть даны: матрица транспортных издержек  , объемы производства
, объемы производства  и объемы потребления
и объемы потребления 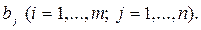
| А | |||||
| С | |||||
| В |
Решение начинаем с проверки баланса:  Далее, строим начальный опорный план по методу северо-западного угла:
Далее, строим начальный опорный план по методу северо-западного угла:
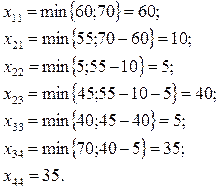
Приступаем к вычислению потенциалов. В таблице издержек для удобства выделим клетки соответствующие плану перевозок.
По соответствующим маршрутам плана указываем стоимость перевозки единицы груза из  го пункта отправки в
го пункта отправки в  й пункт потребления. Принимаем
й пункт потребления. Принимаем  (можно выбрать любое число) и, пользуясь соотношением:
(можно выбрать любое число) и, пользуясь соотношением: 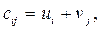 определяем потенциалы
определяем потенциалы

и так далее.

| |||||

| -1 | -6 |
Далее рассчитываем элементы оценочной матрицы по соотношениям:
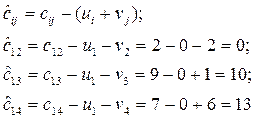
и так далее.
Таким образом

Поскольку в  имеются отрицательные элементы, – план
имеются отрицательные элементы, – план  не является оптимальным.
не является оптимальным.
Приступаем к итерациям. В матрице  , начиная с элемента
, начиная с элемента 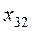 , соответствующего в оценочной матрице наибольшему по абсолютной величине отрицательному элементу, строим цепочку.
, соответствующего в оценочной матрице наибольшему по абсолютной величине отрицательному элементу, строим цепочку.
| – | + | ||||||
| + | – | ||||||
Изменяя элементы, входящие в цепочку, на величину  строим новый план перевозок
строим новый план перевозок 
Снова расставляем потенциалы, используя матрицу транспортных издержек, данную в условиях задачи.

| |||||

| -1 |
И далее строим оценочную матрицу:

В оценочной матрице нет отрицательных элементов, следовательно, план является оптимальным. Таким образом, остается оценить стоимость перевозки в условных единицах.

На этом решение задачи завершается.

|
Поиск по сайту: