АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Алгоритм метода покоординатного спуска решения задачи многомерной минимизации. Геометрическая иллюстрация

Читайте также:
  1. FAST (Методика быстрого анализа решения)
  2. I Психологические принципы, задачи и функции социальной работы
  3. I. 1.1. Пример разработки модели задачи технического контроля
  4. I. 1.2. Общая постановка задачи линейного программирования
  5. I. 2.1. Графический метод решения задачи ЛП
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  8. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  9. I. Ситуационные задачи и тестовые задания.
  10. I. Цель и задачи дисциплины
  11. I.2.4. Алгоритм симплекс-метода.
  12. I.5.3. Подготовка данных для задачи линейного программирования

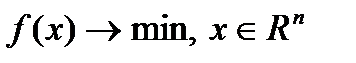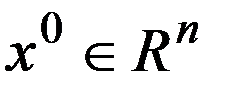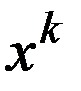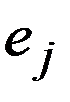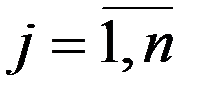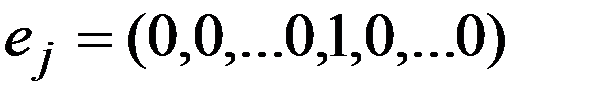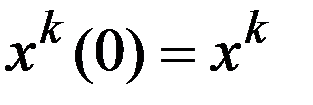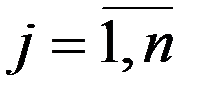
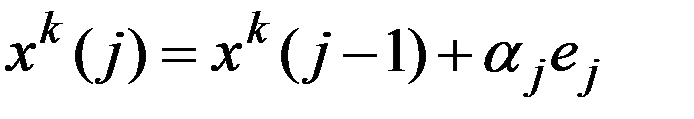Рассм. задачу . Пусть выбрано некоторое начальное приближение. И методом покоординатного спуска было получено приближение . Ч/з , , обозначим координатные вектора (1 на j-ом месте). Положим и для , где 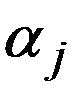определяется из условия 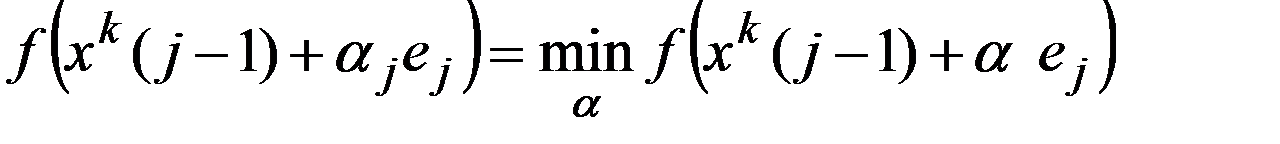. И след. приближение 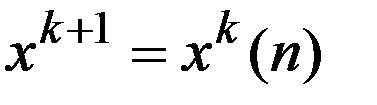, если для некоторого 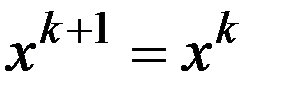, то процесс вычисления заканчивают, А т 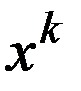считают приближением к точке минимума.

Данный метод хорошо подходит для задач с параллепипедными ограничениями,

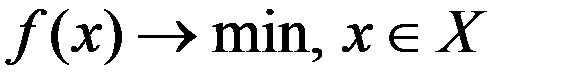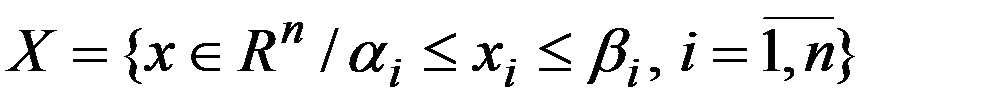, . В этом случае при решении вспомагательной задачи минимизации , .

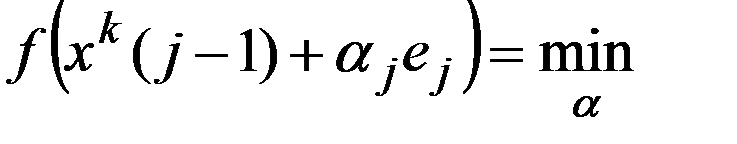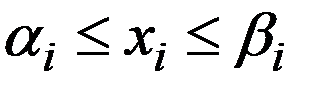на альфа накладываются ограничения, не позволяющие точкам х выходить за пределы мн-ва Х

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)