Случаи интегрируемости ур-ния Эйлера. Примеры

1-й сл. .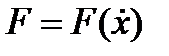

, , т.к. задача явл. вырожденной, тогда

В задаче о кратчайшем расстоянии между 2мя точками плоскасти функционал имеет вид

2й сл. .

В этом сл.ур-е Э-ра , .

Для того, чтобы найти ур-я (1) рассмотрим:

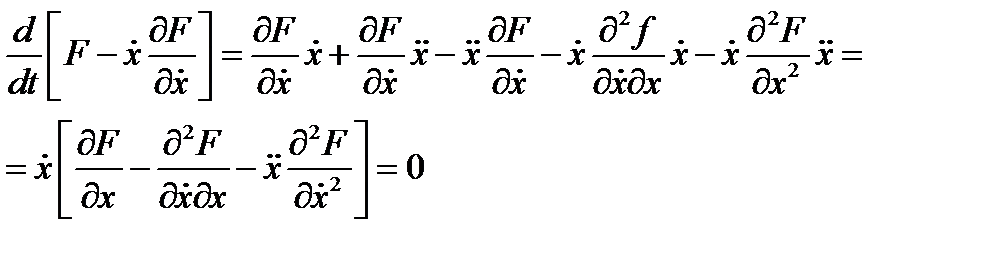
Если ф-я x(t) явл решением ур-я (1), то

Отсюда получим, что первый ур Эйлера в этом случае имеет вид: .

3й сл. .

Тогда ур-е Эйлера им. вид:

4й сл. .

,

Если рав-во (3) не явл тождеством, то оно определяет некоторую линию x=x(t), кот-я удовл-ет граничным условиям лишь в исключит-ых случаях.

Если же ур-е (3) явл тождеством, то подинтегральное выраж-е представляет собой полный дифф-л некоторой ф-и, тогда значение интеграла

Значение интеграла не зависит от вида кривой, соединяющей граничные точки.

Пример. Исследовать на extr функционал

0=0 явл тождеством, значит ф-я подъинтегральная явл полным дифф-м, т.е.

, ,

тогда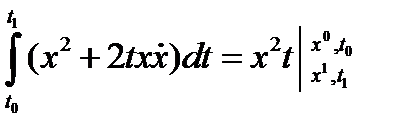

Поиск по сайту: