 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод исключения решения задачи на условный минимум. Пример
Рассм.  (1)
(1)  (2).
(2).
Предпол-ся, что ф-ции  определены и имеют производные 1-го порядка на всем пр-ве
определены и имеют производные 1-го порядка на всем пр-ве  .
.
Если систему ограничений (2) можно представить в виде  , то зад. (1),(2) свод-ся к зад. безусловной минимизации.
, то зад. (1),(2) свод-ся к зад. безусловной минимизации.  .
.
Теорет-я возможность применения такого метода исключ.основывается на т-ие о неявных ф-ях.
Т1 о неявных ф-циях. Пусть рассм. m-мерная ф-ция  .Изв.т.
.Изв.т. 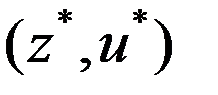 ,для кот.
,для кот. 
 ,тогда сущ. m-мерная ф-я
,тогда сущ. m-мерная ф-я  , уд.усл.: 1)
, уд.усл.: 1) 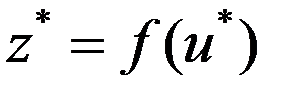 ; 2)
; 2) 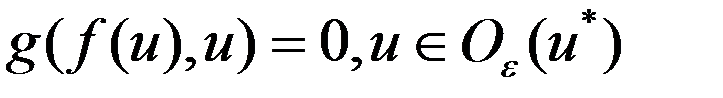 ;3.
;3.  имеет в
имеет в 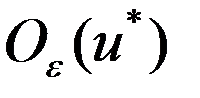 непрер-е производные того же порядка, что и ф-ция
непрер-е производные того же порядка, что и ф-ция  по
по  .
.
Т2. Метод искл.реш-я в з. (1),(2)применим, если в окрестности точки минимума  ф-ции
ф-ции 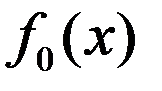 ф-ции
ф-ции  диф-мы и
диф-мы и  .
.
Д-во: Из усл.(3)=>что у м-цы  сущ.хотя бы 1 ненулевой минор порядка m.Предпол-м, что минор распол-ся в первых m строках этой матрицы.В противном случае переобозн. переменные.В принятом предпол-и обозн. Первые m компонент в-ра x через z, а ост-е n-m компонент через в-ор u.Набор ф-ий
сущ.хотя бы 1 ненулевой минор порядка m.Предпол-м, что минор распол-ся в первых m строках этой матрицы.В противном случае переобозн. переменные.В принятом предпол-и обозн. Первые m компонент в-ра x через z, а ост-е n-m компонент через в-ор u.Набор ф-ий 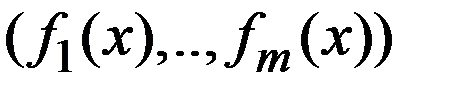 тогда обозн. ч/з
тогда обозн. ч/з  . Тогда система огран-ий
. Тогда система огран-ий  примет вид
примет вид  и для этой ф-ии в т.
и для этой ф-ии в т.  вып-ны все усл. т-мы1.
вып-ны все усл. т-мы1.
Замечание. Возможность прим-ия метода искл. сущ-но огранич-ся сложностью решения с-мы урав-ий  в явном виде.
в явном виде.
Пример1. Исслед. на экстр. ф-ю 
 .
.
 ;
;  ;
;
 ;
; 

(0;-2)-стац точка. 
 -знакопеременна(не вып.необход.усл. 2-го порядка).Т.(0,-2) не явл.экстр-й для ф-ии g..Исх.ф-я экстремума не имеет.
-знакопеременна(не вып.необход.усл. 2-го порядка).Т.(0,-2) не явл.экстр-й для ф-ии g..Исх.ф-я экстремума не имеет.
Поиск по сайту: