Основн. формы ЗЛП. Правила сведения ЗЛП к канон.форме. Геометр.интерпретация ЗЛП. Понятие угловой точки мн-ва

В ЛП выделяют 2 основных формы задачи:

1) Каноническая форма ЗЛП

2) Нормальная форма ЗЛП

Можно перейти от одной задачи к другой.

Любая ЗЛП сводится к канонической с помощью:

1) если в исходной постановке ищется min целевой ф-ии , то –(c,x) превращает исх задачу в задачу о max.

2) если , то соотв ограничения умножаем на (-1), чтобы превратить правую часть в положительную.

3) если m¹0, т.е. в исх постановке присутствуют огранич нер-ва то вводятся и ограничение нер-ва приводят к виду

и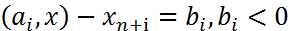

переменные назыв свободными, они характеризуют величину неиспользованного ресурса.

4) если на некот переменную не наложено ограничение на знак, то делают замену c соотв изменением целевой ф-и, если то замена

5) в некот задачах м присутствовать двусторонние прямые ограничения , тогда правое нер-во относится к основным ограничениям и применяют 3)

6) двусторонние прямые огранич вида 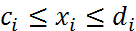сводятся к или 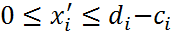соотв изменениями в целевой ф-и

Рассм задачу ЛП внорм форме:

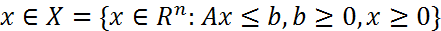
Если множество планов выпуклое, тогда решение сущ., то найдется хотя бы 1 угл.т. мн-ва в которой это решение достигается.

УГЛОВОЙ ТОЧКОЙ мн-ва наз. точка xÎX, кот не может быть представлена как точка отрезка

для любых произв т.

3.Критерий угловой точки множества. Пример.

Рассмотрим задачу в канонической форме: (1), (2).

Теор(Критерий угловой точки): Обозначим ч/з столбцы матр. А, тогда основные ограничения в системе (2) можно записать в виде: . Предположим, что матр.А в системе (2) имеет , т.е. матр.А ненулевая.Для того, чтобы точка была угловой точкой – G необходимо и достаточно, чтобы сущ. , что справедливо рав-во: (3) , если и – ЛНЗ.

Док-во: Необходимость: Пусть – угловая точка этого мн-ва. а) . Т.к. матр. А в соотношении (2) невырождена, то сущ. r ЛНЗ векторов , то выполнено . т.е. (3) справедливо;

б) 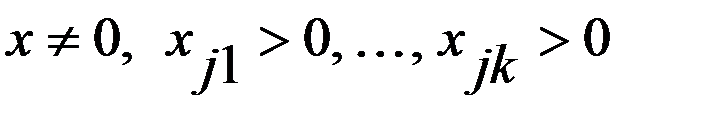тогда основные ограничения в (2) превратятся в равенство: 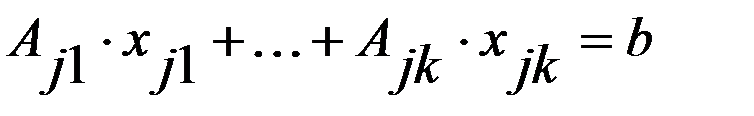(4). Рассм. Рав-во (5). Построим точки и след. обр.:

т.к. ,то к рав-ву (4) прибавим и отнимем рав-во (5) умноженное на 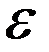получим что выполняются рав-ва:

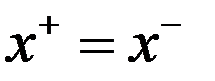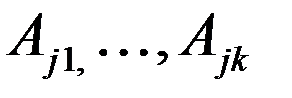, т.е . Легко видеть , но х – угловая точка след-но след-но в (5),т.е.вектора – ЛНЗ след-но

Если , то (3) – доказано, если , то к векторам 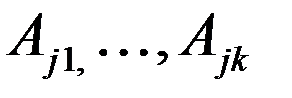можно добавить вектора так, чтобы – ЛНЗ, тогда (3) примет вид: .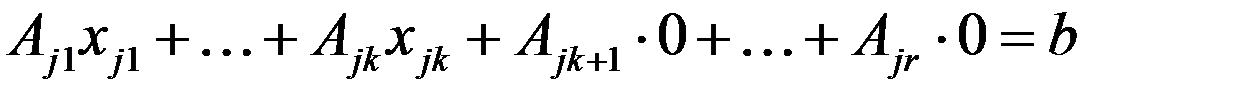

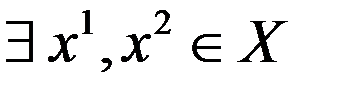Достаточность: пусть для точки справедливо (3): – ЛНЗ, где . Предположим, что , что 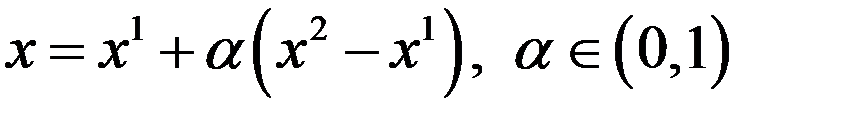(6). Покажем, что (6) возможно только при . Рассмотрим нулевую координату точки х: 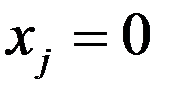, т.е. 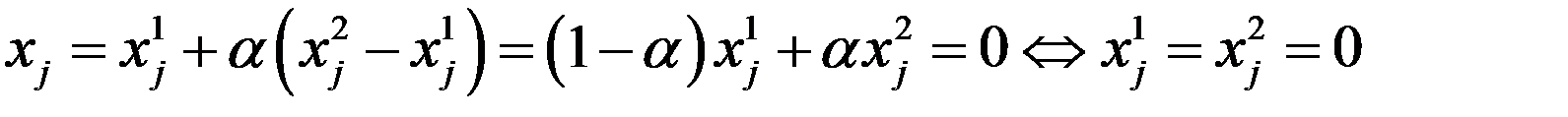. Докажем (6) для тех координат, которые больше 0. Положительными коор-ами т. х могут быть только те, у которых индекс . Пусть 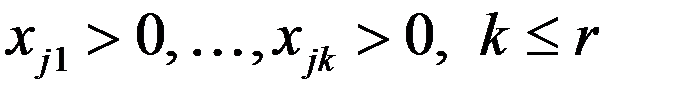Сл. когда или не исключается, тогда система осн-х огр-ий из (2) преобразуется к виду: 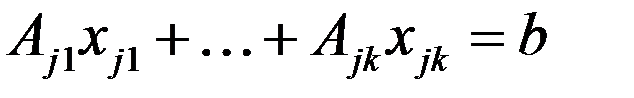. Докажем, что , если . Точки 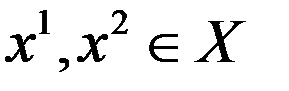было доказано, что 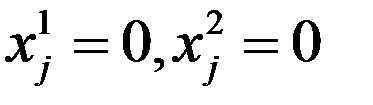, когда 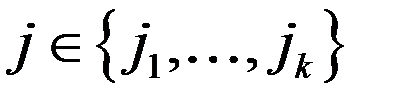след-но и . 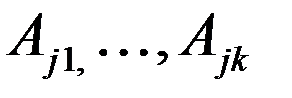Вектора – ЛНЗ, а разложение произвольного вектора пр-ва по ЛНЗ-векторам явл. единственным, след-но для строго пол-ых координат.

Поиск по сайту: