Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации

1)алгоритм метода условного градиента. Пусть задано начальное приближение и методом условного градиента вычислено Строим ф-цию и решаем задачу (1)

Пусть есть решение задачи. Заметим, что 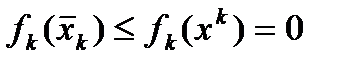. Если 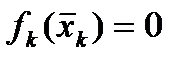, то уд. необходимому усл. и вычислительный процесс заканчивается. Если , то строим отрезок (2) на этом отрезке рассматриваем ф-цию и решаем задачу 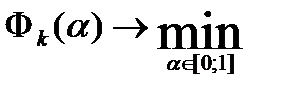(3).

Тогда след.приближение находится по формуле где есть решение задачи (3).

Практическим критерием окончания счета выбираются нер-ва где согласованные числа, характеризующие точность счета.

Замеч1. Метод условного градиента эффективен когда вспомогат. задача (1) допускает простое решение.

Замеч2.Часто на практике задают некоторое значение 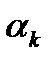, н/р, равное 1, проверяют усл. . Если оно не выполняется, то 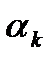уменьшают, например, в два раза и т.д.

2)алгоритм метода проекции градиента. Пусть задано нач. приближение 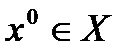и методом проекции градиента вычислено 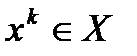. След.приближение ищется по формуле (4) В зависимости от выбора 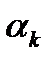строятся различные варианты метода проекции градиента. Например, 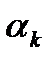может находиться как решение задачи од­номерной минимизации

(5), где (6)

В этом случае при метод проекции градиента превращается в метод скорейшего спуска.

Часто при практическом исп. метода (4) находят такое , что выполняется условие релаксационности

При его нарушении полагают равным снова проверяют условие ре­лаксационности и т. д.

В качестве критерия окончания счета выбираются неравенства , где 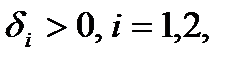— числа, характеризующие точность счета.

Замеч4. Главная сложность реализации метода проекции градиента заключается в решении задачи проектирования.

Поиск по сайту: