Итерация симплекс–метода

Пусть такие номера i, k: и . В силу того, что , а , то знач. цел. ф-ции будет увел.

Т.о. выбирается s () такой, что . Эл. наз. ведущим (разрешающим), i -ая строка и k -ый столбец – ведущими (разрешающими). В качестве знач. перем. . Пост. по ф-лам след.обр.: , , , , , …, , , .

, т.е. n-r коорд. нулев. Не равн. 0 коорд. имеют инд.: 1,..., s -1, s +1,…, r, k. Рассм.лин.комб. (*). Покажем, что (*) может принимать знач. =0 только при усл., что все . Рассм.

, тогда (*) предст. в виде:

. Последняя сумма предст. собой лин. комб. ЛНЗ векторов ; 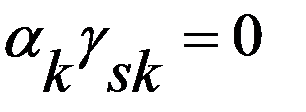, . След-но, вектора стоящие при базисных коорд. точк. - ЛНЗ.

, где ,

Выражая из s -го ур-ния

(**) знач. перем. и подставляя полученное выражение в остальные ур-ния (**) получим зависимость между базисными и небазисными коорд. точк.

9. Обоснование конечности симплекс – алгоритма.

Алгоритм решения з. оптимизации назыв. Конечным, если для его реализации на компе требуется конечное число операций для нахождения оптимального плана.

ЗЛП невырожденная, если все угловые точки мн-ва Х невырожденные.

Теор. Если в невырожд. ЗЛП известна какая-либо угл. т-ка, то отправляясь от нее либо б. найден оптимальный план, либо б. показано, что цел. Ф-я неограниченна и для этого понадобится конечное число итераций.

Док-во. Пусть у – угл. т-ка мн-ва Х. Т.к. ЗЛП невырожд., то . Разрешающий эл-т . Если не вып. достат. усл-е оптимальности , то

Т.е. переход к др. угловой точке происходит со строгим возрастанием, а достигается только в 1 строчке, т.е. выбор координаты, выводимой из базиса однозначный. Число угл. т-к конечно. Из всего этого следует конечность симплекс-алгоритма.

Зам:Если задача ЛП явл вырожденной, то в сл выбора вырожд угл точки х может произойти зацикливание, которое будет явл следств, изменения базиса вырожд угл точки.

10. Обоснование непустоты мн-ва планов в ЗЛП. Пример.

(1)

Рассм след вспомог задачу: Введем в рассм искусств перемен , ()=y≥0. Т.к. мн-во : (2)

И рассм задачу: (3)

В покоординатной форме ограничения (2) им след вид

Замеч: 1). Если вектор ,то система основных ограничений(2)переходит в сис-му основных ограничений (1)

2). Мн-во , т.к.

3). Т. явл. угловой точкой мн-ва Z с базисом

4). Целев ф-ия , т.о. зад (3) – есть ЗЛП в канонической форме, к кот удобно применить симплекс метод, при этом в силу огр-ти целев ф-ии на Z зад (3) обяз-но им решение.

Непустота мн-ва планов

Пусть - реш зад (3) и знач целев ф-ии зад (3).

Возможны 2 случая: 1. ; 2.

Теорема: Если , то угловая точка этого мн-ва.

Док-во:1) Это означает, что вектор y*,..,z* имеет строгополож координаты, тогда мн-во Х явл пустым. Действ, если мн-во Х пустым не явл, то в этом мн-ве найдется некоторая точка y, Ay=b, y≥0. Но тогда т z’=(y,0)пренад Z,а знач цел.ф в ней =0, что против предполож о том, что т z*явл решением задачи.

2) Рассм случай, когда из подстановки в зад (3) полагаем, что и в силу того, что .

Покажем, что -угловая точка X: . Построим точки тогда , но

- угловая точка мн-ва Z, решение ЗЛП (3), полученное симплекс методом послед рав-во возможно, когда -угловая точка мн-ва X.

Поиск по сайту: