Основные определения в задаче одномерной минимизации. Примеры

Рассмотрим задачу:

Считаем, что принимает на X конечные значения. Произвольное решение этой задачи будем обозначать ч/з , мн-во решений ч/з .Таким обр, .

Опр. Посл-ть наз. минимизирующей для ф-ции на мн-ве X, если

Из опр-ния и существования точной нижней грани следует, что минимизирующая последовательность всегда сущ

Опр. Посл-ть сходится к мн-ву X, если , где ч/з обозначено расстояние от точки до мн-ва

Замеч. Если мн-во не явл. пустым, то всегда сущ. минимизирующая посл-ность, сходящаяся к .

Пример1: Пусть , мн-во X совпадает со всей числовой прямой 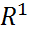. Здесь мн-во решений 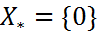, и минимальное значение ф-ции тоже равно нулю. Посл-ть явл. минимизир. т.к. , но к нулю не стремится при .

Опр. Ф-ция 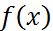наз. унимодальной на , если она непр. на этом отрезке и сущ. такие числа , такие что:

1) строго монотонно убывает при ,

2) 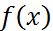строго монотонно возрастает ,

3) при так, что .

Если , функция наз. строго унимодальной.

32.Метод деления отрезка пополам решения задачи одномерной минимизации. Пусть 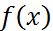-унимодальна. Решим задачу .

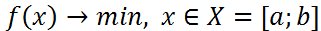Выберем 2 точки: , , где , являющаяся параметром метода, . Чем меньше значение тем больше точность. Заметим чтоточк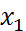и и располагаются симметрично относительно середины отрезка и при малых значениях делят его практически пополам.

Если 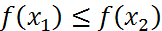, то полагаем

Если , то полагаем

В силу унимодальности отрезок имеет непустое пересечение с множеством решений задачи и длинна нового отрезка равна .

Пусть найден отрезок 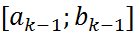, длина кот. . который имеет непустое пересечение с множеством .

Вычисляем точки: ,

и значение ф-ции 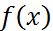в них.

Если 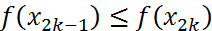, то полагаем

Если , то полагаем

Получим отрезок , который имеет непустое пересечение с мн-вом и его длина равна

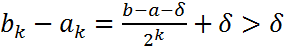
Процесс деления отрезка пополам продолж. до тех пор, пока не будет достигнута заданная точность , при этом будет проведено 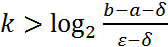итераций.

Так как каждое деление отрезка пополам требует двух вычислений значений ф-ции, то для достижения заданой точности требуется вычислений ф-ции.

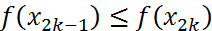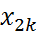После определения отрезка в качестве точки минимума можно взять равное: если , если

И значение даст приближенное значение . При этом погрешность решения, то есть отклонение приближенного решения от мн-а решений не превосходит величины .

Поиск по сайту: