Примеры. 2.Линейная ф-ция одновременно выпукла и вогнута

1. Ф-ция выпукла

2. Линейная ф-ция одновременно выпукла и вогнута.

3. Ф-ция где А – симметричная неотрицательно определенная матрица размерности , и х – вектор размерности n, выпукла

УТВ: сумма пересеч и умнож мн-ва на число явл. выпуклым мн-вами,если исходные мн-ва-выпуклые.

Пустое мн-во и мн-во состоящ из 1 точки удобно считать выпуклыми.

УТВ: сумма выпуклых ф-ций есть вып ф-ия.

Т1 (сво-во неотрицательности остатка) Пусть ф-ция 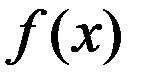явл. выпуклой, дифференцируемой на выпуклом мн-ве Х, тогда выполняется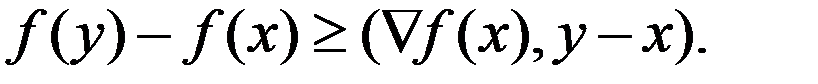

Док-во: Т.к. ф-ция 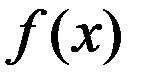явл.выпуклой, то

.

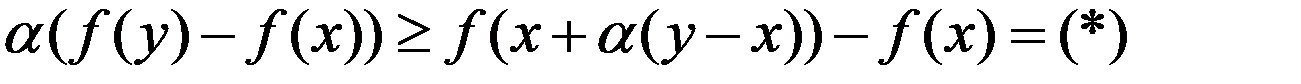
Т.к. ф-ция явл. дифференцируемой, то приращение этой ф-ции можно разложить в ряд Тейлора:

(*)=

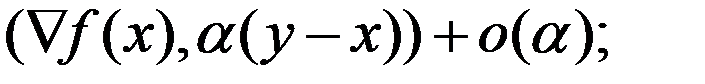
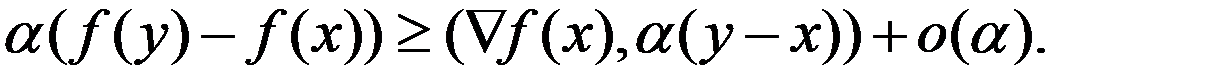
Последнее неравенство делим на и устремим к 0. Теорема доказана.

Поиск по сайту: