АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования

Читайте также:
  1. I. 3.1. Двойственная задача линейного программирования
  2. II.2. Задача о назначениях
  3. II.4. МЕТОД ВЕТВЕЙ И ГРАНИЦ В ЗАДАЧАХ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
  4. VI. Общая задача чистого разума
  5. В задачах 13.1-13.20 даны выборки из некоторых генеральных совокупностей. Требуется для рассматриваемого признака
  6. в задачах экспертного выбора.
  7. В) Задача
  8. В) Задача
  9. В) Задача
  10. В) Задача
  11. В) Задача
  12. В) Задача

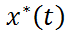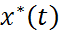Рассм. задачу (1) где определена и непрерывна со всеми частными производными до 2-ого порядка включительно.Ищем (1) при усл. когда отрезок [ ] не фиксирован. Значение ф-ии на концах отрезка не заданы. Пусть явл решением рассм.задачи.Тогда найдётся такие ,что кривая уд. уравн Эйлера и краевым усл. , (2). Определим усл. для значений 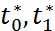. Рассм где - произвольные приращения интервала, . И предположим продолжимость решения 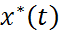на отрезок [ ], если это необходимо. Рассмотрим - (3)

В (4) рассм , разделим на и .

,тогда (4)

, .

(5)

(4) должно выполняться для . Значит (4) и (5) должны выполняться одновременно. Значит:

(6)

В (7) произвольны и независимы друг от друга, поэтому (7)

Т.о. справедлива теор 2.

Теорема 2. Если доставляет слабый минимум функционалу (1) в задаче с незакреплёнными концами, то кривая удовл ДУ Эйлера (2) и усл. (6) и (7).

 


 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)