АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Опр-ия выпуклого мн-ва, выпуклой функции. Св-ва выпуклых множеств. Сумма выпуклых функций. Св-во неотрицательности остатка выпуклой функции

Читайте также:
  1. A) сумма потребительских стоимостей, который может приобрести рабочий на свою номинальную заработную плату
  2. F. Метод, основанный на использовании свойства монотонности показательной функции .
  3. I Психологические принципы, задачи и функции социальной работы
  4. I. Деньги и их функции.
  5. I. Функции
  6. I. Функции эндоплазматической сети.
  7. II. Основные задачи и функции
  8. II. Основные задачи и функции
  9. II. Функции плазмолеммы
  10. III. Предмет, метод и функции философии.
  11. III. Функции и полномочия Гостехкомиссии России
  12. IV. Конструкция бент-функции

(1) (2)

Если ф-ция 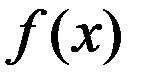явл. выпуклой на выпуклом мн-ве X, то задача (1), (2) наз. задачей выпуклого программирования.

Опр: Мн-во наз выпуклым, если для любых двух точек отрезок, соединяющий эти точки полностью принадлежит этому мн-ву, т.е. Примерами выпуклых мн-в могут служить шар произвольного радиуса, гиперплоскоть, все пр-ва.

Опр: Ф-ция 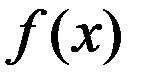, определенная на выпуклом мн-ве Х, наз. выпуклой, если для выполняется (1)

Замеч1: Если мн-во X явл. пустым или состоит из одной точки, то ф-цию, определенную на таком мн-ве, считают выпуклой.

Замеч2: Если знак нерав-ва в (1) заменить на противоположный, то ф-ции наз.вогнутой. При выполнении строгого неравенства ф-ция наз. строго выпуклой (Соответственно строго вогнутой).


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)