АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Обоснование метода ломаных решения задачи одномерной минимизации

Читайте также:
  1. FAST (Методика быстрого анализа решения)
  2. I Психологические принципы, задачи и функции социальной работы
  3. I. 1.1. Пример разработки модели задачи технического контроля
  4. I. 1.2. Общая постановка задачи линейного программирования
  5. I. 2.1. Графический метод решения задачи ЛП
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  8. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  9. I. Ситуационные задачи и тестовые задания.
  10. I. Цель и задачи дисциплины
  11. I.2.4. Алгоритм симплекс-метода.
  12. I.5.3. Подготовка данных для задачи линейного программирования

Метод ломаных применяется для решения задачи (1), без требования унимодальности ф-ции f, но эти ф-ии должны уд. усл. Липшица.

Опр. Говорят, что ф-ция уд.усл. Липшица на [a;b], если , что 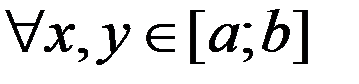. (2) Геометрическое усл.Липшица означает, что угловой коэф-т хорд, кот соединяют две произвольные точки графика ф-ций y=f(x) не превосходит константы L.

Если ф-я уд.усл. Липшица на [a;b] то она явл-ся непрерывной на [a;b].

Т1: Пусть f(x)-определена и непрерывна на [a;b] и на каждом [ai;ai+1], где а=a1<a2<…<an<an+1=b уд. усл. Липшица с конст Li, тогда f(x)уд. усл Лип на всем отр-ке [a;b]с конст L=maxLi.

Д-во: выберем произвольные x,y из отрезка [a,b]. Предположим, что т-ка .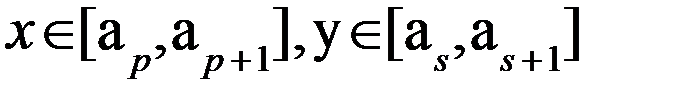

Рассм.модуль разности

Т2: Пусть f(x)–дифер на [a;b] и её производная огр-на на [a;b], тогда эта ф-ция уд. усл. Лип с конст. L=sup|f’(x)|

Д-во: т.к. ф-ция f(x) диф-ма, то по формуле конечных приращений приращение ф-ции

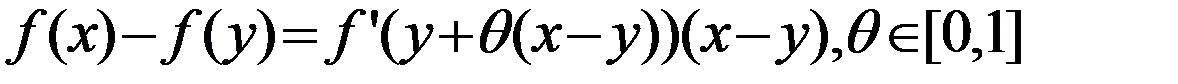
Отсюда и из ограниченности производной следует утв. теоремы.

Пусть ф-я f(x) удовлетворяет на [a;b] условию Липш (2) с константой L. Зафиксируем некоторую точку y из [a;b] и построим ф-цию

,

,

g(y,y)=f(y)

. Ф-ция g явл. кусочно-линейной ф-цией, ее график есть ломаная с углами наклона L (до y) и –L (после y) и в т-ке y g(y,y)=f(y).

Рассмотрим нерав-во т.е. , .


 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)