Примеры задач динамического программирования, их особенности

Динам программирование (ДМ) (динам планирование) – это метод нахождения оптим реш в задаче с многошаг структурой. Многие эконом задачи раздел на шаги естеств образом, это н-р, процессы планир и управления развиваемые во времени. Естеств шагом в них может быть год, квартал, месяц и т.д. Однако МДП может исп при реш задач, где время не фигурирует. Разделение на шаги в таких задачах вводится искусственно, поэтому динамика ЗДП заключ в методе реш-я. К ЗДП относ задачи перспективного и текущ планирования во времени, задача многошагов нахож-я оптимума при размещ производит сил, задачи оптим быстродействия.

Выделим особенности ЗДП:

1. в задаче рассм система, состояния кот в каж мом времени t опред вектором 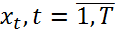. Дальнейшее изменение состояние системы зависит от дан состояния и не зав от того, каким путём система пришла в это состояние. Такие процессы наз проц без последействия.

2. на каж шаге выбирается одно решение (управление) , под действ кот система переходит из предыдущ состояния в след состояние . Это нов сост явл ф-ей сост-я на начало интервала и принятого в начале интервала решения , т.е. . 3 Действ на каж шаге связаны с опред выигрышем (доходом, прибылью) или потерей (издержками), кот зависят от состояний на начало шага и принятого решения.

4. На векторы состояния и управления может быть наложены ограничения, объединение которых представляют область допуст значений.

5. Требуется найти такое допустимое управление для каждого шага t, чтобы получить экстремальн значение ф-ции цели за все Tшагов.

Любую допустимую посл-ть действий для каж шага, переводящую систему из нач состояния в конечное наз стратегией управления. Допуст стратегия управления, доставляющая цели экстрем значение наз оптимальной.

Пример Задача перспективного планирования.

Пусть планируется деятельность группы из Nпромыш предприятий (пр) на перид Тхоз лет. В нач период на развитие системы пр выделены некот ср-ва в кол-ве K, кот д\б распределены между пр. В проц деят пр вложенные в него ср-ва частично амортизируются. Каж пр за год приносит доход в зависит от вложен ср-в, часть которого отчисл в фонд пр. В нач каж хоз года имеющ ср-ва перераспределяются между пр-ями. Возник задачи определения объема ср-в в нач каж года, кот нужно выделить каждому пр-ю чтобы суммарн чистый доход за Т лет был максимальным.

В этой задаче проц принятия решения разбив на Tшагов. Управление этим процессам заключ в нач и последовательном распред ср-в , где есть объем ср-в, выделенных i–ому предпр в нач t–го года. Состояние системы опис вектором , где сост i–го предпр. на нач t–го года. В свою очередь состояние каждого пр-я явл вектором, компонентами кот служат труд ресурсы, осн фонды, фин положение и т.д. Очевидно, что вектор управления есть ф-ция состояния системы на начало соотв периода, т.е. 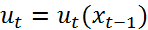. Нач сост системы может быть заданным. В кач целевой ф-ции часто рассм суммарн прибыль объединения пр-й за Т хоз лет. Управление выбирается из некот мн-ва , кот может быть описано как мн-во эконом возможностей, определ различ ограничениями, налагаемыми на состояние системы и вектор управления

Поиск по сайту: