АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение Эйлера

Читайте также:
  1. E) Для фиксированного предложения денег количественное уравнение отражает прямую взаимосвязь между уровнем цен Р и выпуском продукции Y.
  2. IV. УРАВНЕНИЕ ГАМЛЕТА
  3. V2: Волны. Уравнение волны
  4. V2: Уравнение Шредингера
  5. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
  6. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  7. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  8. В простом случае обычное дифференциальное уравнение имеет вид
  9. В этом случае уравнение Эйлера принимает вид
  10. ВКЛАД Эйлера в РАЗВИТИЕ тригонометрии
  11. Влияние температуры на константу равновесия. Уравнение изобары
  12. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона

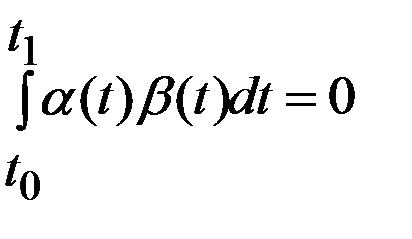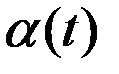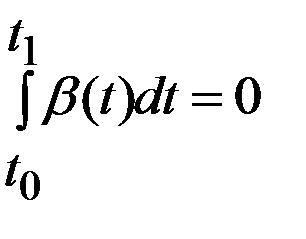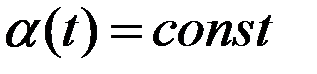Лемма Дюбуа-Реймона. Если рав-во выполнено для некоторой непрерывной ф-ии и всех непрерывных ф-ий , уд.условию , то =с на .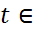

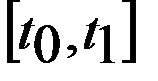Док-во. Пусть 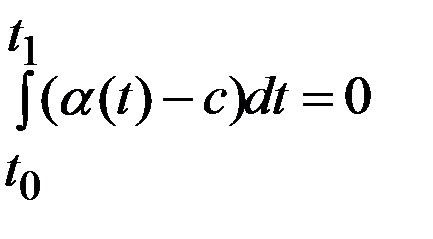. Для ф-ии 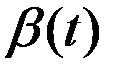, кот.уд.условиям леммы, рассм. 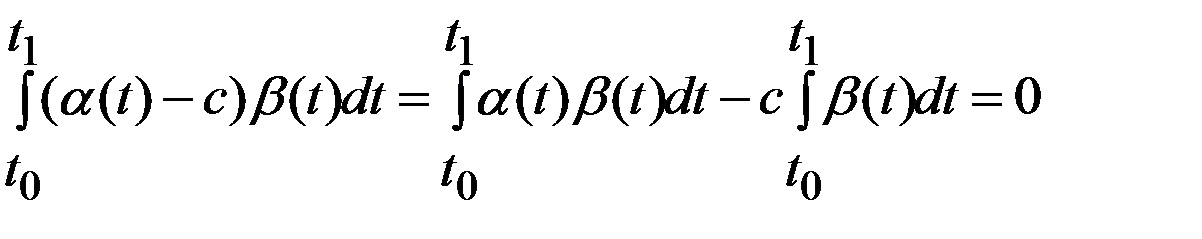. (1). Вместо 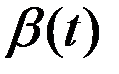в (1) подставим 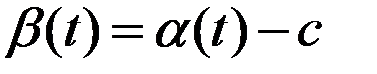. Тогда 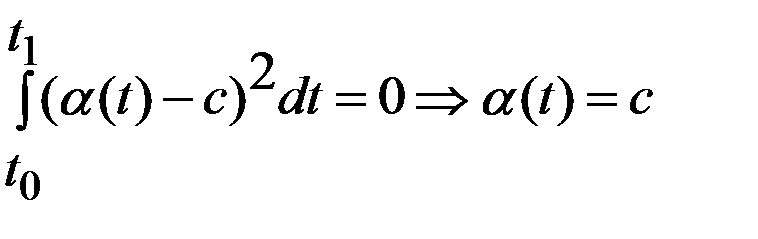, т.к. -непрерывная ф-ия.

Следствие. Если 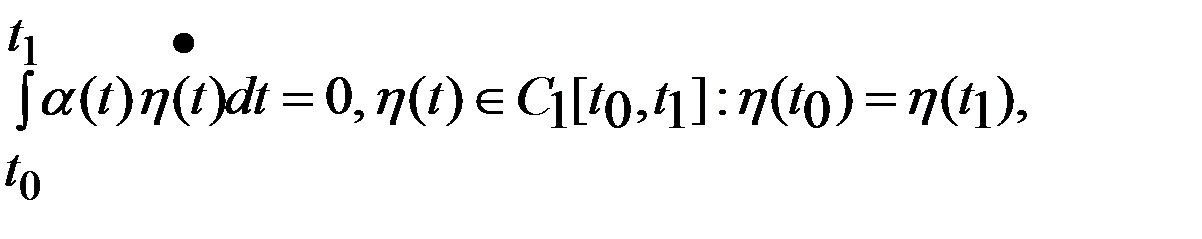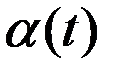-непрерывная ф-ия, то .

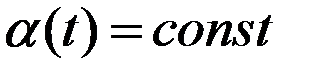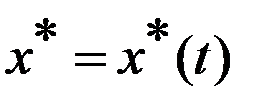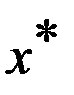Теорема. Пусть кривая явл. минималью в простейшей ЗВИ, то на ней выполнено ДУ Эйлера (2) с краевыми условиями (3). Док-во. Пусть кривая явл минималью ПЗВИ, то ,где 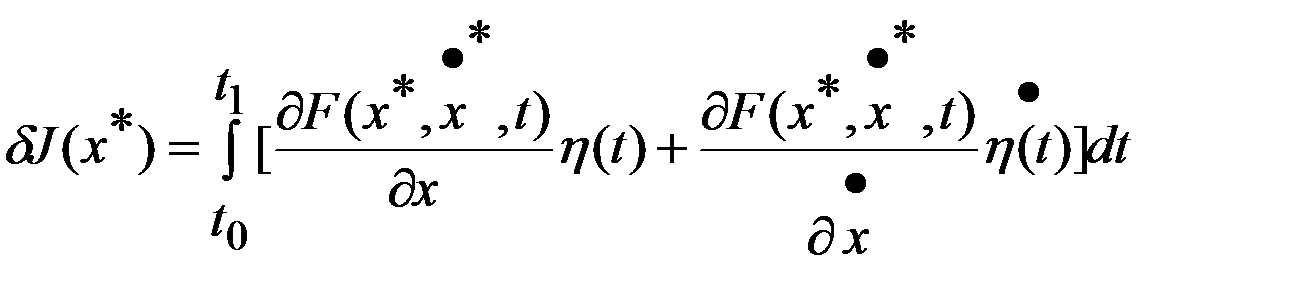, 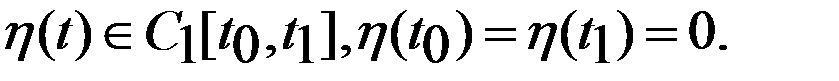Рассмотрим

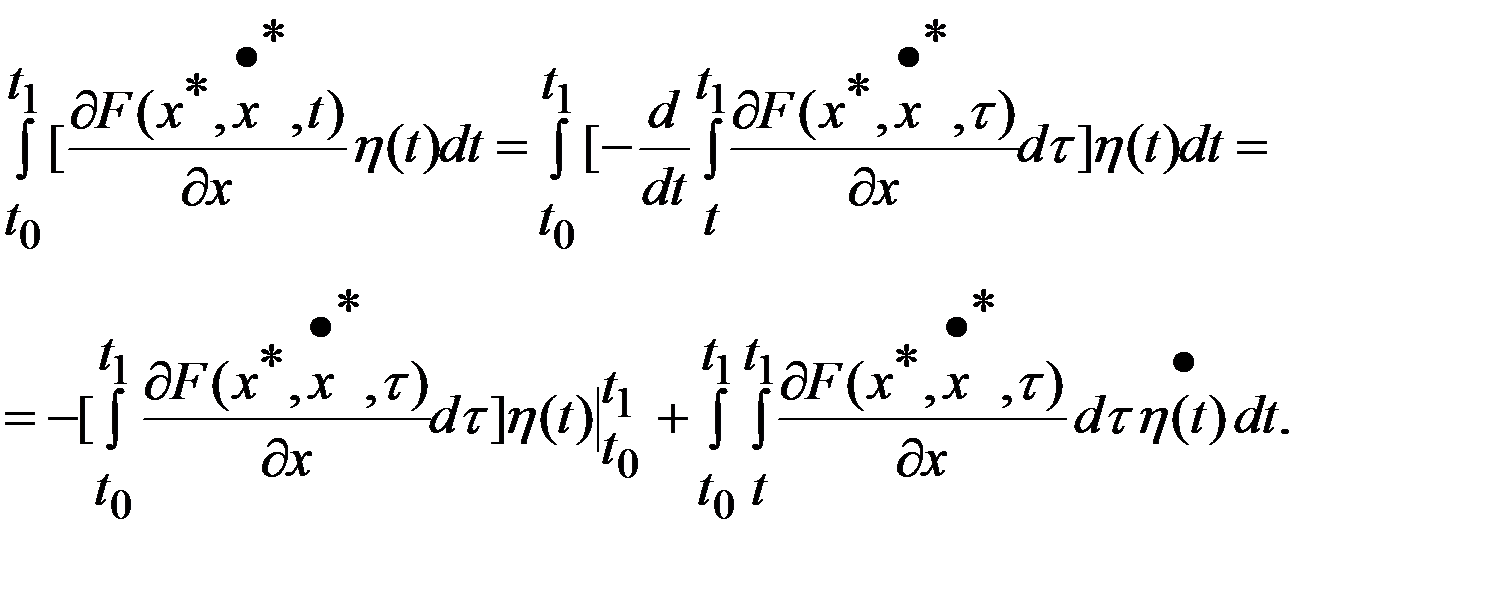
Тогда

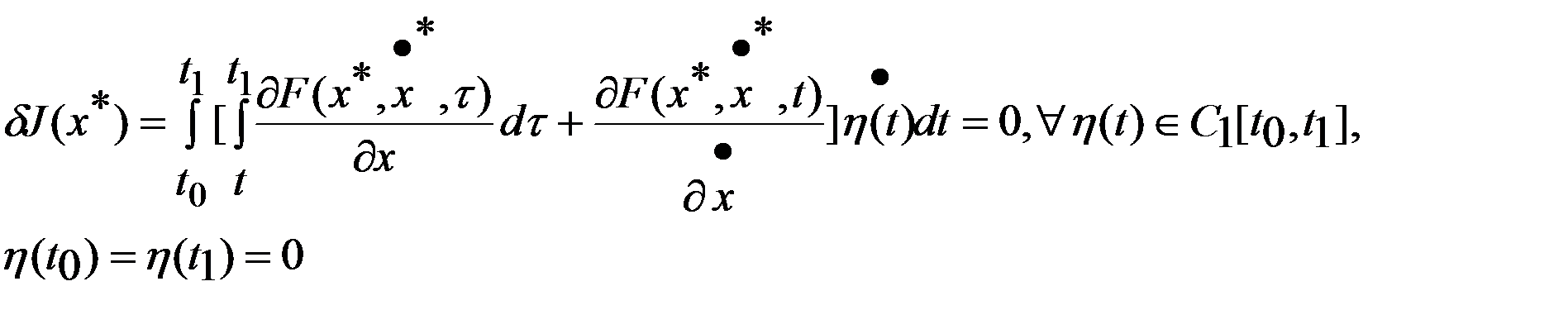Используя следствие к лемме получим (4). Ур-ние (4) наз. интегр.уравн.Эйлера, его решение называется экстремалью. Перепишем (4) так 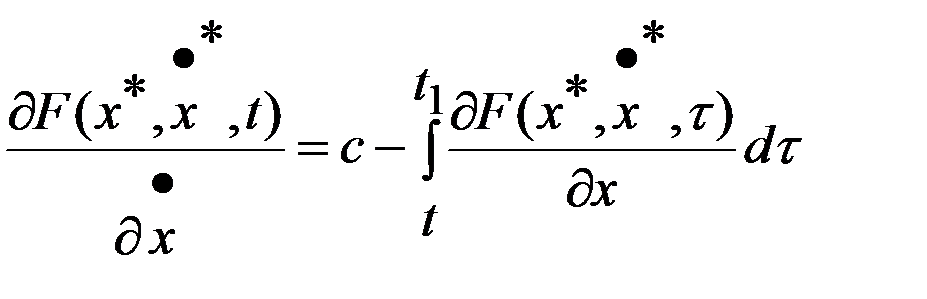. В правойчасти стоит ф-я диф. по t, значит и в левой части стоит ф-я диф. по t,


 


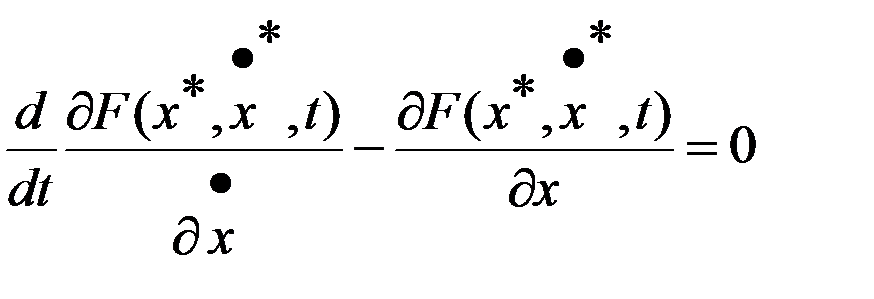
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)