 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции
Теор(о т. мин в-ой ф-ии): Пусть в задаче  (1)
(1)  -(2) ф-ия
-(2) ф-ия 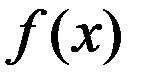 выпукла, определена на выпуклом мн-ве Х, тогда: 1) каждая точка ее локального минимума (если такая сущ-ет), явл-ся точкой глобального минимума;
выпукла, определена на выпуклом мн-ве Х, тогда: 1) каждая точка ее локального минимума (если такая сущ-ет), явл-ся точкой глобального минимума;
2) Мн-во  решений задачи (1), (2) явл-ся выпуклым; 3) если ф-ия
решений задачи (1), (2) явл-ся выпуклым; 3) если ф-ия 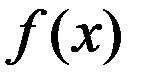 строго выпукла, то она может достичь своего min не более чем в одной точке.
строго выпукла, то она может достичь своего min не более чем в одной точке.
Док-во: 1) Пусть  есть точка глобальн min ф-ии
есть точка глобальн min ф-ии 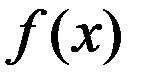 , т.е.
, т.е.  окрестность этой точки
окрестность этой точки  , так что
, так что  Пусть
Пусть  точка
точка  Соединим эти точки отрезком
Соединим эти точки отрезком  Т.к. мн-во Х явл-ся выпуклым, то при всех
Т.к. мн-во Х явл-ся выпуклым, то при всех  :
: 
 при
при  , след-но найдется такое значение
, след-но найдется такое значение 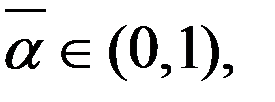 что
что  Поэтому
Поэтому 
 что противоречит тому, что т.
что противоречит тому, что т.  явл-ся точкой локальн min.
явл-ся точкой локальн min.
2) Мн-во 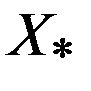 - мн-во решений задачи
- мн-во решений задачи 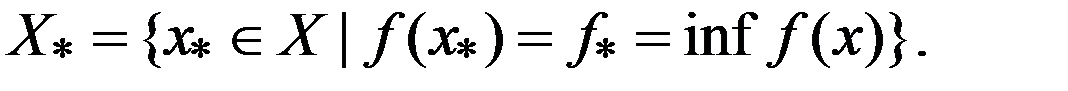 Пусть мн-во
Пусть мн-во  состоит более чем из одной точки. Возьмем
состоит более чем из одной точки. Возьмем 
Рассм.  Т.к.ф-ия
Т.к.ф-ия 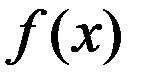 -выпукла, то
-выпукла, то 
 выполняется нер-во
выполняется нер-во

3) Предположим сущ-ет точка 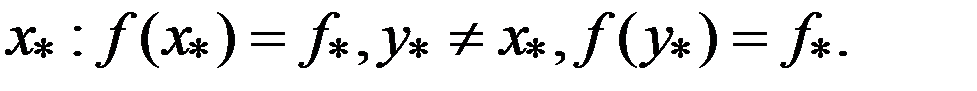 Соединим точки
Соединим точки  и
и  отрезком:
отрезком: 
мы нашли точку  в которой
в которой  что противоречит тому, что
что противоречит тому, что  явл-ся точкой локального min.
явл-ся точкой локального min.
Т 2 (о ст-ной точке в-ой ф-ции): Каждая стационарная точка выпуклой ф-ции  , определенная на выпуклом множестве Х, явл. ее точкой минимума.
, определенная на выпуклом множестве Х, явл. ее точкой минимума.
Док-во: Пусть  стационарная точка ф-ции
стационарная точка ф-ции 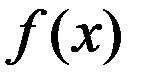 , т.е.
, т.е.  Рассмотрим произвольную точку
Рассмотрим произвольную точку  Для точек
Для точек  в силу выпуклости ф-ции
в силу выпуклости ф-ции 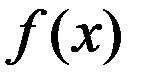 выполняется:
выполняется:  (3)Т.к. ф-ция
(3)Т.к. ф-ция 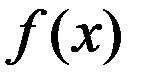 дифференцируема, то приращение (из (3))=>
дифференцируема, то приращение (из (3))=>
 .
.  по св-ву неотр
по св-ву неотр
остатка 
 точка минимума..
точка минимума..
Необходимые усл. минимума дифференцируемой ф-ции на выпуклом мн-ве, выраженные через скалярное произведение. Критерий минимума выпуклой дифференцируемой функции на выпуклом множестве, сформулированный через скалярное произведение.
Замеч1. Если 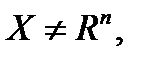 ф-ция
ф-ция  дифференцируема, но не обязательно выпукла, то усл.
дифференцируема, но не обязательно выпукла, то усл.  может не выполняться в точке минимума ф-ции
может не выполняться в точке минимума ф-ции  , т. к. возможна ситуация, когда точка
, т. к. возможна ситуация, когда точка  принадлежит границе мн-ва X.
принадлежит границе мн-ва X.
Теор1. Пусть ф-ция  непрерывно дифференцируема на выпуклом мн-ве X. Если точка
непрерывно дифференцируема на выпуклом мн-ве X. Если точка  явл. ее точкой минимума, то для всех
явл. ее точкой минимума, то для всех  выполняется нерав-во
выполняется нерав-во
 (1)
(1)
Док – во. Пусть  - точка минимума ф-ции
- точка минимума ф-ции  . Тогда сущ.
. Тогда сущ. 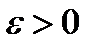 , такое что
, такое что  для всех
для всех  . Выберем произвольную точку
. Выберем произвольную точку  и рассмотрим отрезок
и рассмотрим отрезок
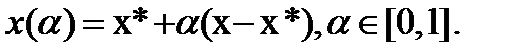
Т. к. мн-во X выпукло, то этот отрезок принадлежит мн-ву X и при малых 
 . Для таких
. Для таких  рассм.
рассм.
 (2)
(2)
Последнее выражение является неотрицательным, так как x* есть тока минимума. Но тогда  как и в противном случае при достаточно малых
как и в противном случае при достаточно малых  приращение (3) изменит свой знак на противоположный. Теор. доказана.
приращение (3) изменит свой знак на противоположный. Теор. доказана.
Следстивие 1. Если 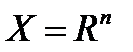 или
или  ,то нер-во (1) превращается в равенство
,то нер-во (1) превращается в равенство 
Следствие 2. Усл(2) можно записать в виде
 (3)
(3)
Теор2. Для того, чтобы выпуклая, непрерывно дифференцируемая ф-ция  , определенна на выпуклом, замкнутом мн-ве Х, достигала своего минимума в точке
, определенна на выпуклом, замкнутом мн-ве Х, достигала своего минимума в точке  , необходимо и достаточно, чтобы выполнялось нерав-во
, необходимо и достаточно, чтобы выполнялось нерав-во 
Док-во: Необходимость следует из теор1. Докажем достаточность. Пусть точка x* такова, что выполнена усл.  Возьмем произвольную точку
Возьмем произвольную точку  и рассмотрим
и рассмотрим 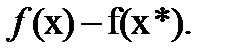 По св-ву неотрицательного остатка имеем
По св-ву неотрицательного остатка имеем
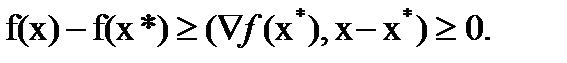
Замечание 4. Форма (3) необходимого усл. минимума непрерывно дифференцируемой ф-ции на выпуклом замкнутом мн-ве используется для построения метода усл. градиента.
24.Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
Опр. Расстояние от точки  до мн-ва
до мн-ва  определ. формулой
определ. формулой  .Ф-ция
.Ф-ция  непр. по y.
непр. по y.
Опр. Проекцией точки y на мн-во X наз. такая точка  , для кот.
, для кот. 
Задача нахождения точки p наз задачей проектирования точки y на мн-во X. Если решение задачи проектирования  , то норма
, то норма 
 Задачу проектир. обычно заменяют равносильной задачей
Задачу проектир. обычно заменяют равносильной задачей  (1)
(1)
Задача (1) предст. собой задачу min-ции квадратичной ф-ции
Утв1. Если мн-во  явл. Замкнутым и не пустым, то
явл. Замкнутым и не пустым, то 

 и если
и если  , то
, то 
Док-во. Пусть  . В противном сл.
. В противном сл.  . Рассм. произв. точку
. Рассм. произв. точку  и построим мн-во
и построим мн-во  . Мн-во
. Мн-во  не явл. пустым, явл. замкнутым и огранич. Поэтому по теор. Вейерштрасса
не явл. пустым, явл. замкнутым и огранич. Поэтому по теор. Вейерштрасса  проекция точки y на Z. В силу постр. мн-ва Z:
проекция точки y на Z. В силу постр. мн-ва Z:  . Пусть
. Пусть 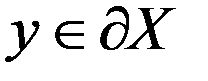

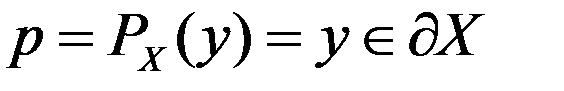 ,
,  .
.
Предп. противное.  . Тогда
. Тогда  . Рассм. отрезок, соед. точки y и p:
. Рассм. отрезок, соед. точки y и p: 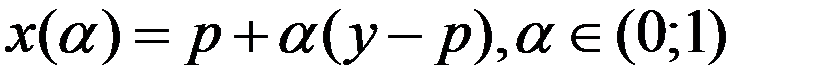 . Найдется такое
. Найдется такое 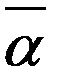 , что при
, что при 
 . Рассм. расстояние
. Рассм. расстояние 
След-но, p не явл. проекцией.
Утв2. Если  непустое, выпуклое и замкнутое, то
непустое, выпуклое и замкнутое, то 
 ед. проекция
ед. проекция 
Док-во. Пусть 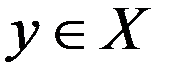 . Тогда очевидно, что
. Тогда очевидно, что  , поэтому явл. ед. Рассм., когда
, поэтому явл. ед. Рассм., когда  . Предп., что
. Предп., что  более одной проекции
более одной проекции  ,
,  ,
, 
Вектора  не явл. коллинеарными. Действ-но, если
не явл. коллинеарными. Действ-но, если  , то
, то  . Если
. Если  , то
, то  . Это противоречит тому, что
. Это противоречит тому, что  .Рассм.
.Рассм. 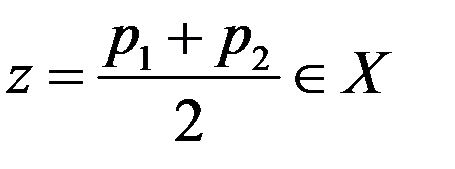 .
. 
Нашли точку 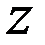 , такую
, такую  , что противор., что
, что противор., что 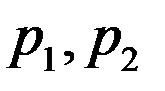 -проекции. Замеч. Если мн-во не явл. выпуклым, то может сущ. две проекции. Рассм. примеры нахождения проекций точек на мн-ва для некот. конкр. мн-в
-проекции. Замеч. Если мн-во не явл. выпуклым, то может сущ. две проекции. Рассм. примеры нахождения проекций точек на мн-ва для некот. конкр. мн-в 
1)  ; 2)
; 2) 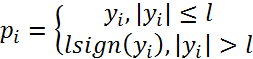 ;
; 
 ; 3)
; 3) 
 ; 4)
; 4) 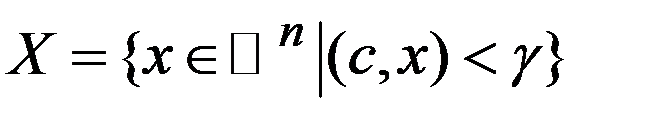
Т.к. проекция в любой точке, не принадл. X, будет принадл. границе мн-ва X, то от данной задачи можно перейти к задаче min-ции ф-ции f (x) при ограничении  . Т.к. c -ненулевой вектор, сост. классич. ф-цию Лагранжа
. Т.к. c -ненулевой вектор, сост. классич. ф-цию Лагранжа 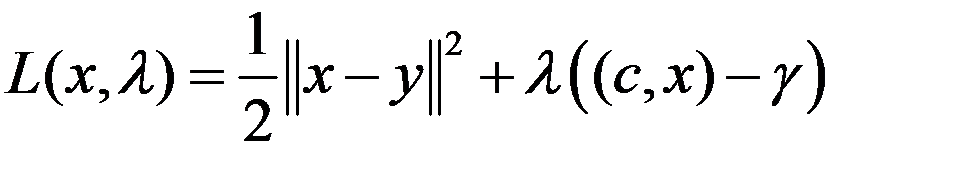 .Система необх. усл:
.Система необх. усл:  ;
; 
25. Критерий построения проекции на выпуклое замкнутое множество. Необходимые усл. минимума диф. ф-ции на выпуклом мн-ве, выраженные в терминах проекции точки на мн-во. Критерий минимума выпуклой диф. ф-ции на выпуклом мн-ве, сформулированный с помощью оператора проектирования.
Теор1. Пусть непустое мн-во X явл. выпуклым и замкнутым. Тогда точка р явл. проекцией 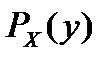 точки у на мн-во X только тогда, когда выполняется усл.
точки у на мн-во X только тогда, когда выполняется усл.  для всех
для всех  .
.
Док-во. Рассм. ф-цию 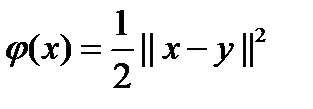 . Эта ф-ция явл. квадратичной, выпуклой. Мн-во X по усл. Тео. замкнуто и выпукло. Поэтому
. Эта ф-ция явл. квадратичной, выпуклой. Мн-во X по усл. Тео. замкнуто и выпукло. Поэтому  достигается в точке
достигается в точке  эта точка явл.единственной. Тогда по теореме о необходимых и достаточных условиях минимума выпуклой ф-ции на замкнутом, выпуклом мн-ве выполняется усл.
эта точка явл.единственной. Тогда по теореме о необходимых и достаточных условиях минимума выпуклой ф-ции на замкнутом, выпуклом мн-ве выполняется усл.  для всех
для всех  .
.
Но в данном случае  Тем самым теор. доказана.
Тем самым теор. доказана.
В следующих теоремах выясняется зависимость решения задачи математического программирования и решения задачи проектирования.
Теор2. Пусть точка  есть точка локального минимума ф-ции
есть точка локального минимума ф-ции  на множестве X. Функция
на множестве X. Функция  предполагается непрерывно дифференцируемой, а мн-во X выпуклым и замкнутым. Тогда для произвольного
предполагается непрерывно дифференцируемой, а мн-во X выпуклым и замкнутым. Тогда для произвольного  справедливо равенство
справедливо равенство  . Док-во. Пусть
. Док-во. Пусть  . Тогда выполняется усл.
. Тогда выполняется усл.  (1) Пусть
(1) Пусть  . Преобразуем последнее равенство к виду
. Преобразуем последнее равенство к виду  и подставим в формулу (1). Получим
и подставим в формулу (1). Получим  . Тогда по теор1 заключаем, что
. Тогда по теор1 заключаем, что  . Теорема доказана.
. Теорема доказана.
Теор3. Пусть ф-ция  явл. выпуклой, непрерывно дифференцируемой, мн-во X выпуклым и замкнутым. Точка
явл. выпуклой, непрерывно дифференцируемой, мн-во X выпуклым и замкнутым. Точка  есть точка локального минимума
есть точка локального минимума  для произвольного
для произвольного  справедливо рав-во
справедливо рав-во  .
.
Док-во. Необходимость следует из теоремы 2.
Докажем достаточность. Пусть выполняется усл.  . Тогда по теореме 1 имеем
. Тогда по теореме 1 имеем  из чего следует
из чего следует 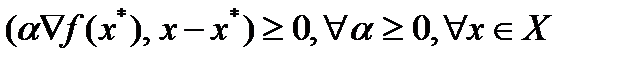 и
и  .
.
Тогда по критерию локального минимума выпуклой ф-ции на замкнутом выпуклом мн-ве заключаем, что  есть точка локального минимума ф-ции
есть точка локального минимума ф-ции  на мн-ве Х. Теорема доказана.
на мн-ве Х. Теорема доказана.
26. Теорема о седловой точке функции Лагранжа (достаточные условия оптимальности).
Рассм.задачу  (1),
(1), 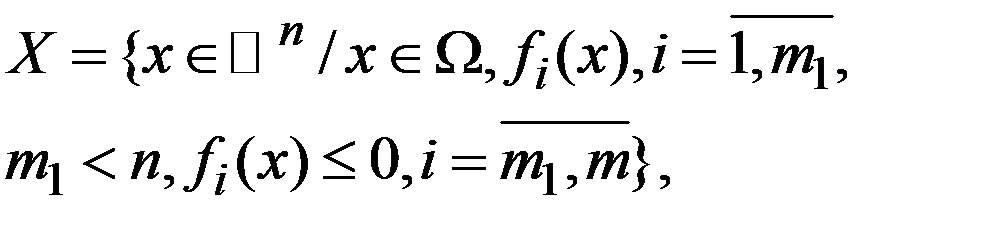 (2)
(2)
где  - заданное мн-во и ф-ии
- заданное мн-во и ф-ии 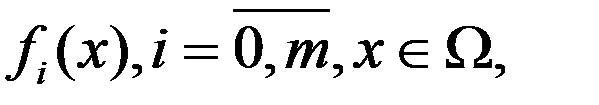 определены на
определены на  .
.
Для задачи (1), (2) рассмю нормированную ф-цию Лагранжа:  (3) определенную на мн-ве
(3) определенную на мн-ве 

 (4)
(4)
Опр. Точка  наз. седловой точкой функции Лагранжа (3), в области
наз. седловой точкой функции Лагранжа (3), в области  , если
, если 
Теорема1 (о седловой точке ф-ии Лагранжа) Пусть точка  явлю с едловой точкой ф-ции Лагранжа (3), тогда
явлю с едловой точкой ф-ции Лагранжа (3), тогда  явлюрешение задачи (1)-(2).
явлюрешение задачи (1)-(2).
Док-во: 1. Покажем сначала, что в условия теоремы точка  уд. ограничениям (2) задачи (1)-(2). Т.к.
уд. ограничениям (2) задачи (1)-(2). Т.к. 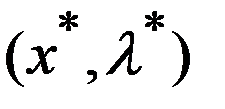 -седловая точка ф-ции Лагранжа, то выполняется нер-ва:
-седловая точка ф-ции Лагранжа, то выполняется нер-ва:
 (5)
(5)
Рассмю левое из (5):  (6)
(6)
В нер-во (6) подставляем

 вып-ся огранич. рав-ва.
вып-ся огранич. рав-ва.
Выберем некоторый индекс  положим
положим  остальные
остальные  . Подставим это в (6):
. Подставим это в (6): 
 выполняются ограничения неравенства.
выполняются ограничения неравенства.
Точка  , т.к. она является седловой точкой функции Лагранжа. Т.е.
, т.к. она является седловой точкой функции Лагранжа. Т.е.  удовл-ет огр-ям задачи (1)-(2).
удовл-ет огр-ям задачи (1)-(2).
2. Покажем, что для значения  выполняется условие дополнительной нежесткости, а имеено, если
выполняется условие дополнительной нежесткости, а имеено, если 
Предположим противное: пусть для некоторого индекса 
 В нер-ве (6) положим
В нер-ве (6) положим  , тогда получим
, тогда получим  последнее нер-во будет вып-ся для
последнее нер-во будет вып-ся для  а не для
а не для 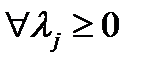 что противоречит определению седловой точки.
что противоречит определению седловой точки.
3. Покажем, что точка  -решение задачи (1)-(2). Рассмотрим правое из нер-в (5), из которого в силу условия дополнительной нежесткости
-решение задачи (1)-(2). Рассмотрим правое из нер-в (5), из которого в силу условия дополнительной нежесткости 
Рассмотрим последнее нер-во для 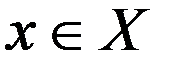 :
:
 Доказан
Доказан
27. Критерий существования седловой точки функции Лагранжа для задачи выпуклого программирования.
Рассм.задачу  (1),
(1),  (2)
(2)
где  -заданное мн-во и ф-ии
-заданное мн-во и ф-ии  определены на
определены на  .
.
Для задачи (1), (2) рассм. нормированную ф-ию Лагранжа:  (3) определенную на мн-ве
(3) определенную на мн-ве


 (4)
(4)
Теор2 (Критерий сущ.седловой точки ф-ии Лагранжа для задачи выпуклого прогр-ния) Пусть в задаче (1)-(2) функции  являются выпуклыми, т.е задача (1)-(2)-задачи выпуклого программирования, (
являются выпуклыми, т.е задача (1)-(2)-задачи выпуклого программирования, ( -выпуклое мн-во) и функции
-выпуклое мн-во) и функции  явл. дифференцируемыми в точке
явл. дифференцируемыми в точке 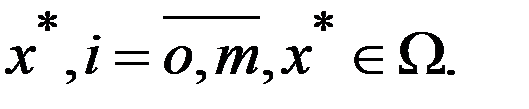 Тогда точка
Тогда точка  явл.седловой точкой ф-ции Лагранжа тогда и только тогда, когда
явл.седловой точкой ф-ции Лагранжа тогда и только тогда, когда

Док-во: (Необходимость). Пусть точка  - седлова точка ф-ии Лагранжа, тогда
- седлова точка ф-ии Лагранжа, тогда  Т.к. ф-ии
Т.к. ф-ии  диф-мы, то ф-ия Лагранжа диф-ма:
диф-мы, то ф-ия Лагранжа диф-ма:

Последнее нер-во разделим на  ,
, 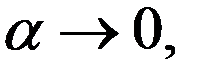 получим (5)
получим (5)
Покажем, что для значения  вып-ся условие доп-ной нежесткости, а именно, если
вып-ся условие доп-ной нежесткости, а именно, если 
Предположим противное: пусть для некоторого индекса 
 В нер-ве (6) положим
В нер-ве (6) положим  , тогда получим
, тогда получим  последнее нер-во будет вып-ся для
последнее нер-во будет вып-ся для  а не для
а не для 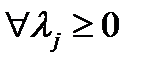 что противоречит определению седловой точки.
что противоречит определению седловой точки.
Достаточность: Пусть вып-ся соотношения (5)-(6), покажем тогда, что точка  явл-сяседловой точкой ф-ии Лагранжа. Т.к. ф-ии
явл-сяседловой точкой ф-ии Лагранжа. Т.к. ф-ии  -выпуклые по условию теоремы, то ф-ия Лагранжа выпуклая по х.
-выпуклые по условию теоремы, то ф-ия Лагранжа выпуклая по х.
По св-ву неотр-ти остатка для выпуклой ф-ии вып-ся:

т.е. правая точка из опр. седловой точки. Точка 
а из условия (6)
 отсюда следует правая часть нер-ва из определения седловой точки. Теорема доказана.
отсюда следует правая часть нер-ва из определения седловой точки. Теорема доказана.
28. Определение двойственной задачи к задаче математического программирования.

где 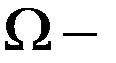 заданное мн-во, ф-ции
заданное мн-во, ф-ции  определены на мн-ве
определены на мн-ве  Переформулируем задачу (1) при помощи нормальной классической ф-ции Лагранжа:
Переформулируем задачу (1) при помощи нормальной классической ф-ции Лагранжа:  Ф-ция Лагранжа определяется на мн-ве
Ф-ция Лагранжа определяется на мн-ве  . Переформулируем задачу (1) при помощи нормальной классической ф-ции Лагранжа:
. Переформулируем задачу (1) при помощи нормальной классической ф-ции Лагранжа: 
Ф-ция Лагранжа определена на мн-ве  Рассм. Ф-цию
Рассм. Ф-цию


Рассм. задачу  .
.
Точную нижнюю грань 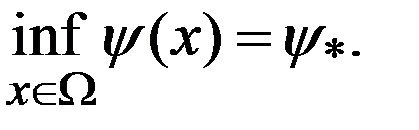 В силу зависимости ф-ии
В силу зависимости ф-ии  с задачей (1):
с задачей (1):  В предположении, что
В предположении, что  и мн-во решений задачи (1) не пусто, т.е.
и мн-во решений задачи (1) не пусто, т.е.  Задача (3) то же будет иметь мн-во решений
Задача (3) то же будет иметь мн-во решений  с тем же min значением.
с тем же min значением.
Аналогично с функцией (2) рассмотрим ф-цию  которая будет определена на
которая будет определена на  И рассм. задачу
И рассм. задачу 
Задача (4) наз. двойственной к задаче (3) или к задаче (1). Переменные  двойственные переменные,
двойственные переменные,  наз. основными.
наз. основными.
При подстановке задачи (1) предполаг., что ф-ия  приним. Конечные значения на мн-ве
приним. Конечные значения на мн-ве  , поэтому ф-ия
, поэтому ф-ия  . Однако определение ф-ии
. Однако определение ф-ии  не исключает возможности принятия значений разных
не исключает возможности принятия значений разных  . Чтобы подчеркнуть конечность ф-ии
. Чтобы подчеркнуть конечность ф-ии  говорят, что рассматривается задача
говорят, что рассматривается задача  (5)
(5)
где  Обозначим
Обозначим  и через
и через 
Теор Для  имеет место нер-во
имеет место нер-во  (6)
(6)
Док-во: По определению функции 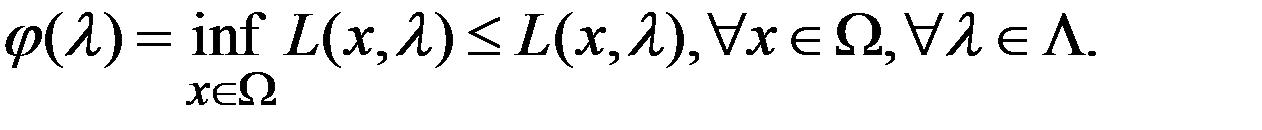 Если
Если 
то  Переходя в последнем нер-ве к точной нижней грани по мн-ву
Переходя в последнем нер-ве к точной нижней грани по мн-ву  , получаем нер-во
, получаем нер-во  Остальные два нер-ва в (6) очевидны.
Остальные два нер-ва в (6) очевидны.
Теорема доказана.
29. Связь между двойственной и прямой задачами математического программирования.
Имеется задача(1): 
Которую можно переформулировать в(2):  (2)
(2)
Рассм. задачу двойственную к (2). Пусть

Двойственная задача имеет вид: 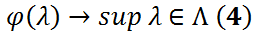
Теор: Для  им. место нер-во
им. место нер-во

Док-во: По опр-ию ф-ии  . Если
. Если 
То  Переходя в последнем нер-ве к точной нижней грани по мн-ву
Переходя в последнем нер-ве к точной нижней грани по мн-ву  , получаем нер-во
, получаем нер-во  .Остальные два нер-ва в (5) очевидны. Теорема доказана.
.Остальные два нер-ва в (5) очевидны. Теорема доказана.
Теорема. Если задачи (2) и (4) имеют решение, т.е. мн-во  то ф-я Лагранжа
то ф-я Лагранжа  имеет седловую точку на мн-ве
имеет седловую точку на мн-ве  и обратно, если
и обратно, если  имеет седловую точку, то задачи (2) и (4) имеют решение.
имеет седловую точку, то задачи (2) и (4) имеют решение.
Док-во. Необходимость. Пусть задачи (2) и (4) имеют решение, т.е. выполнено (5). Возьмем т.  . Покажем, что т.
. Покажем, что т.  седловая точка ф-ии Лагранжа.
седловая точка ф-ии Лагранжа.
Рассм. значение 
Выполняется усл. седловой точки, т.к.  т.е.
т.е. 
Достаточность. Пусть ф-я Лагранжа имеет седловую точку  , т.е.
, т.е. 

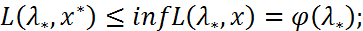

Т.о.  , т.е. задача имеет решение.
, т.е. задача имеет решение.
Следствие1. След. утв. равносильны:
1.Т.  -седловая точка
-седловая точка  на
на 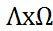 .
.
2. Задачи (2) и (4) имеют решение, т.е. 
3.Сущ. такие  что
что 
4. Справедливо равенство 
Следствие2. Если  и
и  - седловые точки ф-ии
- седловые точки ф-ии  на
на  , то точки
, то точки  и
и  -седловые точки ф-ии Лагранжа, причем значения ф-ии
-седловые точки ф-ии Лагранжа, причем значения ф-ии  во всех этих точках равны между собой.
во всех этих точках равны между собой.
Поиск по сайту: