 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Достаточное условие оптимальности в ЗЛП. Достаточное условие неразрешимости ЗЛП
И сходную задачу  ,
, 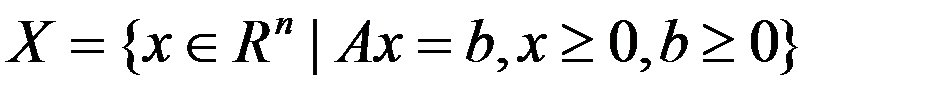 можно переформулировать след. обр.: найти максимум ф-ции
можно переформулировать след. обр.: найти максимум ф-ции 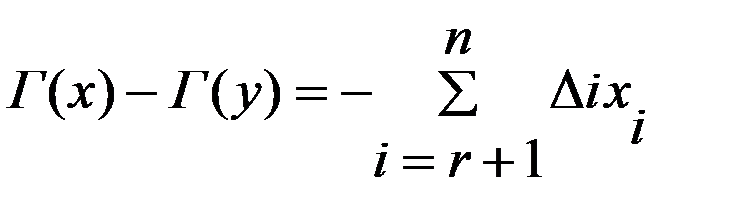 , где
, где 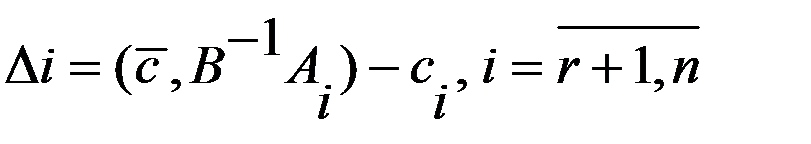 при ограничениях:
при ограничениях: 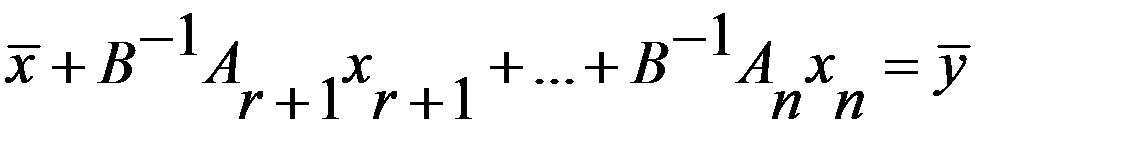 ,
,
где 
и неотрицательности.
Будем искать некот. точку 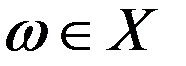 , в которой
, в которой 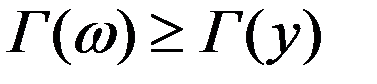 не уменьшится по сравнению с найденным знач. в точке y.
не уменьшится по сравнению с найденным знач. в точке y.
Выберем некот. небазисную перем.  ,
,  и будем подбирать для нее неотрицат. значения. Остальные базисные перем.
и будем подбирать для нее неотрицат. значения. Остальные базисные перем. 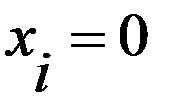 ,
, 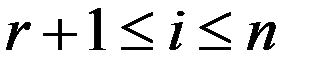 ,
,  . Тогда соотнош.
. Тогда соотнош. 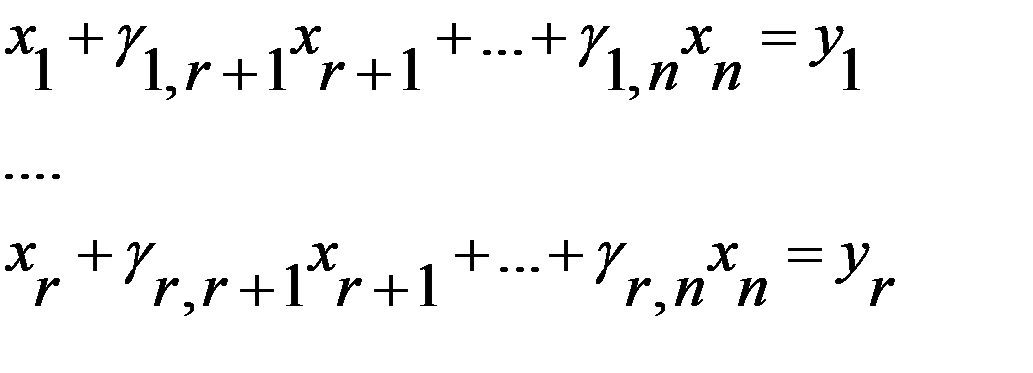
примет вид:  , а выражение целевой ф-ции
, а выражение целевой ф-ции 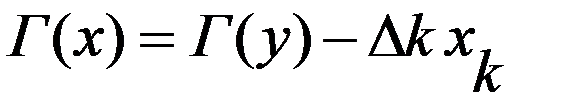 .
.
Достаточное усл. оптимальности: Т.: Если 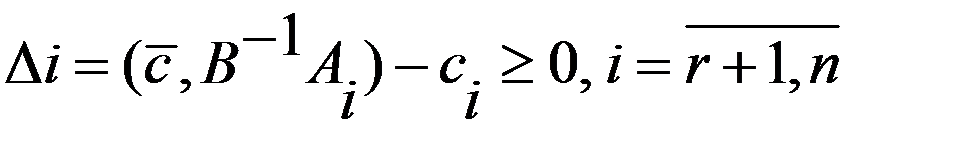 , то план y является оптимальным.
, то план y является оптимальным.
Рассм. произв. точку 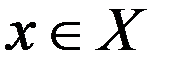 и целев. ф-ю
и целев. ф-ю 
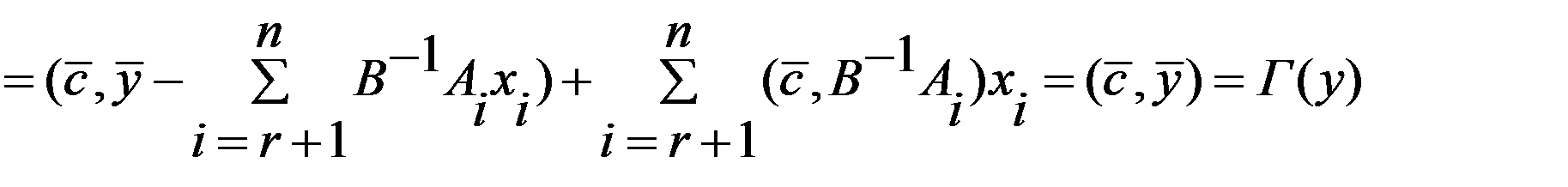 Достаточное усл. неразрешимости:
Достаточное усл. неразрешимости:
Т.: Если найдется небазисная переменная точки упри 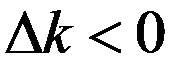 ,к=r+1,n
,к=r+1,n 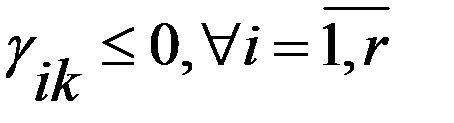 , то целевая ф-ция неограниченно возрастаетна Х.
, то целевая ф-ция неограниченно возрастаетна Х.
Док-во: в усл. Теор. Любой выбор полож. Небаз. Коорд. Приводит к построению точки, удовлт. Всем огр-ниям задачи, увеличивая только знач Хк, а остал оставляя без изм-ия, можно неогр увелич зн целевой ф-ции.
Поиск по сайту: