 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Выпуклая оптимизация. Условие выпуклости. Субградиентный метод выпуклой оптимизации. Метод растяжения пространства. Метод эллипсоидов
Основная задача выпуклого программирования
Пусть задано выпуклое и замкнутое множество  . Рассмотрим множество
. Рассмотрим множество
 .
.
где  (
( ) — вогнутые (выпуклые вверх) непрерывные на
) — вогнутые (выпуклые вверх) непрерывные на  скалярные функции. В теории математического программирования каждый элемент
скалярные функции. В теории математического программирования каждый элемент  принято называть допустимым планом, а само множество X — множеством допустимых планов.
принято называть допустимым планом, а само множество X — множеством допустимых планов.
Формальная постановка задачи выпуклого программирования
Задачу
 ,
,
где  выпукла, а X определяется вышеприведенными условиями, называется основной задачей выпуклого программирования.
выпукла, а X определяется вышеприведенными условиями, называется основной задачей выпуклого программирования.
0 означает, что ставится задача:
Если существует минимальное значение функции  на множестве X, то среди всех допустимых планов найти оптимальный план
на множестве X, то среди всех допустимых планов найти оптимальный план  , для которого
, для которого

при этом число 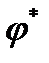 называют значением задачи.
называют значением задачи.
Если оптимального плана не существует, то требуется
· либо найти значение задачи как точную нижнюю грань значений функции  на множестве X:
на множестве X:

· либо убедиться, что  неограничена снизу на множестве X;
неограничена снизу на множестве X;
· либо убедиться в том, что множество допустимых планов X пусто.
Для решения предложенной оптимизационной задачи следует выполнить следующие действия:
· Определить множество  .
.
· Определить вектор-функцию  и вектор
и вектор  .
.
· Определить множество допустимых планов  .
.
· Привести задачу к стандартной форме основной задачи выпуклого программирования и определить оптимизируемую функцию  .
.
· Проверить, является ли полученная оптимизационная задача ЗВП, для этого
· проверить на выпуклость множество X;
· проверить на выпуклость функцию  .
.
В случае успеха п.
· Построить функцию Лагранжа полученной ЗВП.
· С помощью дифференциальных условий Куна-Таккера найти седловые точки построенной функции Лагранжа.
В случае неудачи п. попытаться найти другие методы решения задачи.
Методы субградиентной оптимизации. Эти итеративные процедуры формируют последовательность векторов  . Начиная с некоторого начального значения l 0 эти вектора меняются по следующему правилу
. Начиная с некоторого начального значения l 0 эти вектора меняются по следующему правилу
 ,
,
где xk — оптимальное решение задачи  , а tk — размер шага. Фундаментальный теоретический результат заключается в том, что
, а tk — размер шага. Фундаментальный теоретический результат заключается в том, что
 .
.
Размер шага на практике обычно выбирают, следуя,
 ,
,
Где  — скаляр,
— скаляр, 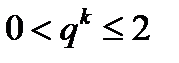 и
и  — верхняя граница для n(D). Обычно
— верхняя граница для n(D). Обычно  получают эвристикой для P. В методе ветвей и границ
получают эвристикой для P. В методе ветвей и границ 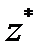 — текущий рекорд. Последовательность
— текущий рекорд. Последовательность  , как правило, начинается с
, как правило, начинается с  и затем
и затем  делится пополам, через фиксированное число итераций, зависящее от размерности задачи.
делится пополам, через фиксированное число итераций, зависящее от размерности задачи.
Поиск по сайту: