Метод наискорейшего спуска. При использовании метода наискорейшего спуска на каждой итерации величина шага аk выбирается из условия минимума функции f(x) в направлении спуска

При использовании метода наискорейшего спуска на каждой итерации величина шага а_k выбирается из условия минимума функции f(x) в направлении спуска, т. е.
.

Это условие означает, что движение вдоль антиградиента происходит до тех пор, пока значение функции f(x) убывает. С математической точки зрения на каждой итерации необходимо решать задачу одномерной минимизации по а функции
.

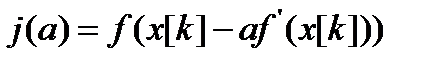Алгоритм метода наискорейшего спуска состоит в следующем.

1. Задаются координаты начальной точки х [0].

2. В точке х [ k ], k = 0, 1, 2,... вычисляется значение градиента f’(x [ k ] ).

3. Определяется величина шага a _k, путем одномерной минимизации по а функции j (a) = f(x [ k ] - af'(x [ k ] )).

4. Определяются координаты точки х [ k+ 1]:

х_i [ k+ 1] = x_i [ k ] – а_kf’_i(х [ k ] ), i = 1,..., п.

5. Проверяются условия останова стерационного процесса. Если они выполняются, то вычисления прекращаются. В противном случае осуществляется переход к п. 1.

В рассматриваемом методе направление движения из точки х [ k ] касается линии уровня в точке x [ k+ 1] (Рис. 2.9). Траектория спуска зигзагообразная, причем соседние звенья зигзага ортогональны друг другу. Действительно, шаг a _k выбирается путем минимизации по а функции φ (a) = f(x [k] - af'(x [ k ] )). Необходимое условие минимума функции d j (a)/da = 0. Вычислив производную сложной функции, получим условие ортогональности векторов направлений спуска в соседних точках:

d j (a)/da = -f’(x [ k+ 1] f’(x [ k ] ) = 0.

Градиентные методы сходятся к минимуму с высокой скоростью (со скоростью геометрической прогрессии) для гладких выпуклых функций. У таких функций наибольшее М и наименьшее m собственные значения матрицы вторых производных (матрицы Гессе)

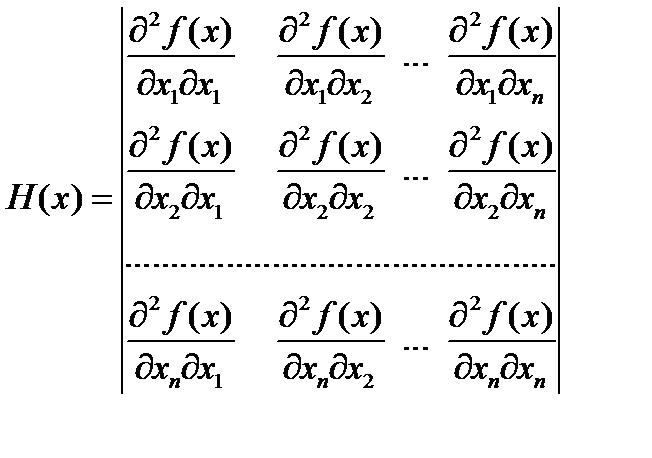
мало отличаются друг от друга, т. е. матрица Н(х) хорошо обусловлена. Напомним, что собственными значениями l_i, i =1, …, n, матрицы являются корни характеристического уравнения

Однако на практике, как правило, минимизируемые функции имеют плохо обусловленные матрицы вторых производных (т/М << 1). Значения таких функций вдоль некоторых направлений изменяются гораздо быстрее (иногда на несколько порядков), чем в других направлениях. Их поверхности уровня в простейшем случае сильно вытягиваются, а в более сложных случаях изгибаются и представляют собой овраги. Функции, обладающие такими свойствами, называют овражными. Направление антиградиента этих функций (см. Рис. 2.10) существенно отклоняется от направления в точку минимума, что приводит к замедлению скорости сходимости.

Поиск по сайту: