Общая постановка задачи

К экономическим задачам оптимизационного типа относятся задачи, в которых требуется найти наилучшее или оптимальное решение при заданных условиях производства. Такие задачи называются задачами на максимум или минимум. Особенностью задач оптимизационного типа является многовариантность их решений, обусловленная следующими причинами: взаимозаменяемостью ресурсов; взаимозаменяемостью готовых видов продукции; существованием альтернативных технологий производства; неодинаковостью технико-экономических показателей даже однотипных хозяйственных субъектов.

Возможны два подхода к постановке оптимизационных задач: при первом подходе требуется получить максимальные конечные результаты при заданных условиях производства; при втором подходе требуется получить заданные конечные результаты при минимальных затратах ресурсов.

Математический инструментарий, позволяющий решать экономические задачи оптимального типа, называется программированием. Различают линейное и нелинейное программирование.

На практике наибольшее распространение получило линейное программирование.

Методы линейного программирования в математике известны под названием общей задачи линейного программирования.

Аналитическая формулировка общей задачи линейного программирования

Общая задача линейного программирования формулируется следующим образом:

Найти решение , позволяющее максимизировать или минимизировать целевую функцию при условиях

Это развернутая запись общей задачи линейного программирования.

Сокращенная запись этой модели имеет вид:

Найти решение , позволяющее максимизировать (минимизировать) функцию

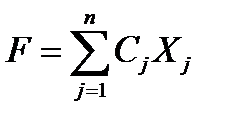
при условиях

Вышеприведенные записи общей задачи линейного программирования называют аналитической формой записи.

Любое решение, удовлетворяющее условиям, называется допустимым решением. Допустимое решение систем неравенств, удовлетворяющее целевой функции, называется оптимальным решением. Такое решение единственно при заданных условиях.

Матричная форма записи общей задачи линейного программирования

при ограничениях

где ;

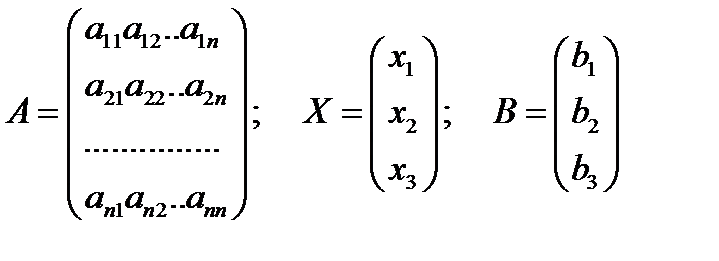
где С – матрица-строка

А – матрица системы

Х – матрица-столбец переменных

В – матрица-столбец свободных членов

Векторная форма записи общей задачи линейного программирования

при ограничениях

где СХ – скалярное произведение векторов

и ,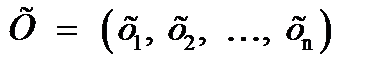

векторы

состоят соответственно из коэффициентов при переменных и свободных членов (про функционал).

В общем случае задача оптимизации формулируется как задача отыскания max или min значения для .

Под решением такой задачи понимается такое , что для остальных элементов выполняется неравенство или в зависимости от требований задачи. При этом:

– некоторая функция

– функционал вида

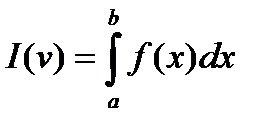
Многокритериальная оптимизация. Методы сведения многокритериальной задачи к однокритериальной. Метод уступок. Методы определения уровня предпочтений. Способы поиска паретовского множества альтернатив.

Многокритериальная оптимизация представляет собой минимизацию некого вектора целей F(x), на которой могут быть наложены дополнительные ограничения или предельные значения:

Отметим, что поскольку F(x) является неким вектором, то любые компоненты F(x) являюся конкурирующими и отсутствует некое единое решение поставленной задачи. Взамен этого, для описания характеристик целей вводится концепция множества точек неулучшаемых решений (так называемая оптимальность по Паретто). Неухудшаемое решение есть такое решение, в котором улучшение в одной из целей приводит к некому ослаблению другой. Для более точной формулировки данной концепции рассмотрим некую область допустимых решений в параметрическом пространстве , которое удовлетворяет всем принятым ограничениям, т.е.

при ограничениях

Отсюда возможно определить соответствующую область допустимых решений для пространства целевых функций .

, где при условии

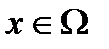
Точка неулучшаемого решения может быть определена как:

Определение. Точка является неулучшаемым решением, если для некоторой окрестности нет некого такого, что и

Поиск по сайту: