 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Примеры решения задач оптимизации методом Гомори
Задача: Для приобретения нового оборудования предприятие выделяет 19 ден.ед. Оборудование должно быть размещено на площади, не превышающей 16 кв.м. Предприятие может заказать оборудование двух видов: машины типа “А” стоимостью 2 ден.ед., требующие производственную площадь 4 кв.м и обеспечивающие производительность за смену 8 т продукции, и машины типа “В” стоимостью 5 ден.ед., занимающие площадь 1 кв.м и обеспечивающие производительность за смену 6 т продукции.
Требуется составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность.
Решение: Обозначим через x1, x2 количество машин соответственно типа “А” и “В”, через L - их общую производительность. Тогда математическая модель задачи:
max L = 8x1 + 6x2
при ограничениях
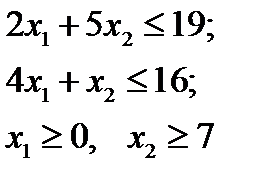
x1, x2 - целые числа
решаем задачу симплексным методом без учета целочисленности.
| C0 | Б0 | Х0 | - | - | ||
| Х1 | Х2 | Х3 | Х4 | |||
| - | Х3 | - | ||||
| - | Х4 | - | ||||
| zi | - | - | - | - | ||
| Di | -8 | -6 | - | - |
| C1 | Б1 | Х1 | - | - | ||
| Х1 | Х2 | Х3 | Х4 | |||
| - | Х3 | - | 9/2 | -1/2 | ||
| Х1 | 1/4 | - | 1/4 | |||
| zi | - | |||||
| Di | - | -4 | - |
| C2 | Б2 | Х2 | - | - | - | ||
| Х1 | Х2 | Х3 | Х4 | S1 | |||
| Х2 | 22/9 | - | 2/9 | -1/9 | - | ||
| Х1 | 61/18 | - | -1/18 | 5/18 | - | ||
| zi | 376/9 | 8/9 | 14/9 | - | |||
| Di | - | - | 8/9 | 14/9 | - | ||
| 4/9 | - | - | 2/9 | 8/9 | -1 |
Получен оптимальный нецелочисленный план Хопт = (61/18;22/9). Lmax = 376/9.
Т.к. у компоненты плана х2 максимальная дробная часть:
max(4/9;7/18) = 4/9, то дополнительное ограничение записываем по первой строке.
22/9 - [22/9] = (2/9 - [2/9])x3 + (-1/9 - [-1/9])x4 - S1, S1  0
0
22/9 - 2 = (2/9 - 0)x3 + (-1/9 - (-1))x4 - S1, S1 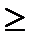 0
0
4/9 = 2/9x3 + 8/9x4 - S1, S1 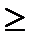 0 - первое ограничение Гомори.
0 - первое ограничение Гомори.
Составленное ограничение дописываем к имеющимся в симплексной таблице.
После построения дополнительного ограничения имеем новую задачу линейного программирования, в которой 3 ограничения. Для получения опорного плана этой задачи необходимо найти третий базисный вектор. Для этого определяем:
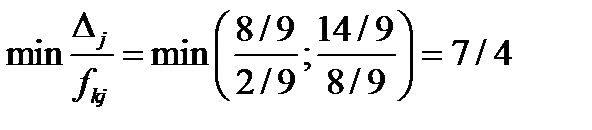 , следовательно, в базис вводим вектор х4.
, следовательно, в базис вводим вектор х4.
Рассчитываем величину  . Минимальное значение
. Минимальное значение  получено по дополнительной строке, значит, не прибегая к искусственной переменной, получаем опорный план расширенной задачи.
получено по дополнительной строке, значит, не прибегая к искусственной переменной, получаем опорный план расширенной задачи.
| C3 | Б3 | Х3 | - | - | - | - | ||
| Х1 | Х2 | Х3 | Х4 | S1 | S2 | |||
| Х2 | 5/2 | - | 1/4 | - | -1/8 | - | ||
| Х1 | 13/4 | - | -1/8 | - | 5/16 | - | ||
| - | X4 | 1/2 | - | - | 1/4 | -9/8 | - | |
| zi | 1/2 | - | 7/4 | - | ||||
| Di | - | - | 1/2 | - | 7/4 | - | ||
| 1/2 | - | - | 1/4 | - | 7/8 | -1 |
Найденный план оптимален, но нецелочисленный. Строим новое ограничение Гомори.
Т.к. максимальная дробная часть среди компонент плана равна 1/2, записываем дополнительное ограничение по первой строке (можно и по третьей).
5/2 - [5/2] = (1/4 - [1/4])x3 + (-1/8 - [-1/8])S1 - S2, S2 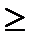 0
0
1/2 = 1/4x3 + 7/8S1 - S2, S2 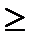 0 - второе ограничение Гомори
0 - второе ограничение Гомори
Это ограничение добавляем в последнюю симплексную таблицу.
Получили задачу, в которой 4 ограничения, следовательно, в базисе должно быть 4 единичных вектора.
Определяем вектор, вводимый в базис: 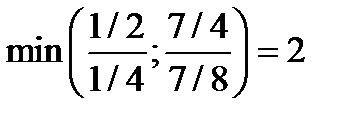 . Можно ввести либо x3, либо S1. Введем вектор S1.
. Можно ввести либо x3, либо S1. Введем вектор S1.
Тогда значение 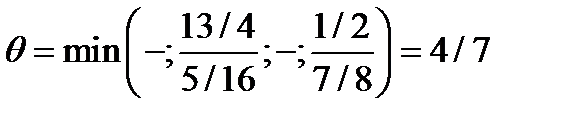 соответствует дополнительному ограничению.
соответствует дополнительному ограничению.
| C4 | Б4 | Х4 | - | - | - | - | - | ||
| Х1 | Х2 | Х3 | Х4 | S1 | S2 | S3 | |||
| Х2 | 18/7 | - | 2/7 | - | - | -1/7 | - | ||
| Х1 | 43/14 | - | -3/14 | - | - | 5/14 | - | ||
| - | X4 | 8/7 | - | - | 4/7 | - | -9/7 | - | |
| - | S1 | 4/7 | - | - | 2/7 | - | -8/7 | - | |
| zi | - | - | - | - | |||||
| Di | - | - | - | - | - | - | |||
| 4/7 | - | - | 2/7 | - | - | 6/7 | -1 |
Получаем новый оптимальный нецелочисленный план. Учитывая замечание 1, вычеркиваем строку и столбец, соответствующие переменной S1.
В полученном плане максимальную дробную часть имеет компонента х2, поэтому записываем дополнительное ограничение по первой строке.
4/7 = 2/7х3 + 6/7S2 - S3, S3 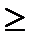 0 - третье ограничение Гомори.
0 - третье ограничение Гомори.
Определяем вектор, вводимый в базис:  . Это вектор х3. Минимальное значение q = 2, что соответствует дополнительной строке.
. Это вектор х3. Минимальное значение q = 2, что соответствует дополнительной строке.
После проведения очередных симплексных преобразований получили:
| C5 | Б5 | Х5 | - | - | - | - | - | ||
| Х1 | Х2 | Х3 | Х4 | S2 | S3 | S4 | |||
| Х2 | - | - | - | -1 | - | ||||
| Х1 | 7/2 | - | - | - | -3/4 | - | |||
| - | X4 | - | - | - | - | -3 | - | ||
| - | X3 | - | - | - | -7/2 | - | |||
| zi | - | - | - | - | |||||
| Di | - | - | - | - | - | - | |||
| 4/7 | - | - | - | - | - | 1/4 | -1 |
План Х5 - оптимальный нецелочисленный.
Дополнительное ограничение запишем по второй строке:
1/2 = 1/4S3 - S4, S4 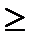 0 - четвертое ограничение Гомори.
0 - четвертое ограничение Гомори.
Т.к. базисной компонентой может быть S3, определяем величину 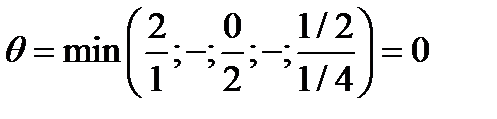 .
.
Минимальное значение получилось по 3 строке, а не по строке Гомори, следовательно, переходим к М-задаче: введем дополнительную переменную х5 в ограничение Гомори.
| C5 | Б5 | Х5 | - | - | - | - | - | -M | ||
| Х1 | Х2 | Х3 | Х4 | S2 | S3 | S4 | X5 | |||
| Х2 | - | - | - | -1 | - | - | ||||
| Х1 | 7/2 | - | - | - | -3/4 | - | - | |||
| - | X4 | - | - | - | - | -3 | - | - | ||
| - | X3 | - | - | - | -7/2 | - | - | |||
| -M | X5 | 1/2 | - | - | - | - | - | 1/4 | -1 | |
| zi | 40-M/2 | - | - | -M/4 | M | -M | ||||
| Di | - | - | - | - | -M/4 | M | - |
| C6 | Б6 | Х6 | - | - | - | - | - | -M | ||
| Х1 | Х2 | Х3 | Х4 | S2 | S3 | S4 | X5 | |||
| Х2 | - | - | -1/2 | 1/2 | - | - | - | |||
| Х1 | 7/2 | - | - | 3/8 | -1/8 | - | - | - | ||
| - | S3 | - | - | - | - | 1/2 | -3/2 | - | - | |
| - | X3 | - | - | 7/4 | -9/4 | - | - | - | ||
| -M | X5 | 1/2 | - | - | - | -1/8 | 3/8 | - | -1 | |
| zi | 40-M/2 | - | M/8 | 2-3M/8 | - | M | -M | |||
| Di | - | - | - | M/8 | 2-3M/8 | - | M | - |
| C7 | Б7 | Х7 | - | - | - | - | - | ||
| Х1 | Х2 | Х3 | Х4 | S2 | S4 | S5 | |||
| Х2 | 4/3 | - | - | -1/3 | - | 4/3 | - | ||
| Х1 | 11/3 | - | - | 1/3 | - | -1/3 | - | ||
| - | X3 | - | - | - | -6 | - | |||
| - | S2 | 4/3 | - | - | - | -1/3 | -8/3 | - | |
| zi | 112/3 | - | 2/3 | - | 16/3 | - | |||
| Di | - | - | - | 2/3 | - | 16/3 | - | ||
| 2/3 | - | - | - | 1/3 | - | 2/3 | -1 |
Дробная часть = max(1/3; 2/3) = 2/3, следовательно, дополнительное ограничение записываем по второй строке.
2/3 = 1/3х4 + 2/3S4 - S5,S5 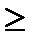 0 - пятое ограничение Гомори.
0 - пятое ограничение Гомори.
Вектор, вводимый в базис: 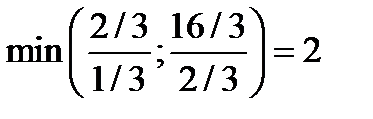 , вводим х4.
, вводим х4.
Тогда значение 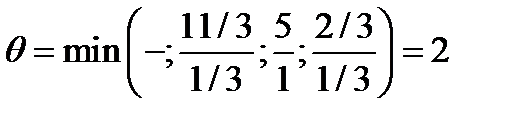 соответствует строке Гомори.
соответствует строке Гомори.
| C8 | Б8 | Х8 | - | - | - | - | ||
| Х1 | Х2 | Х3 | Х4 | S4 | S5 | |||
| Х2 | - | - | - | -1 | ||||
| Х1 | - | - | - | -1 | ||||
| - | X3 | - | - | - | -8 | |||
| - | X4 | - | - | - | -3 | |||
| zi | - | - | ||||||
| Di | - | - | - | - |
План Х8 = (3; 2; 3; 2) - оптимальный целочисленный. Lmax = 36.
Экономическая интерпретация: согласно полученному решению предприятию необходимо закупить 3 машины типа "А" и 2 машины типа "В". При этом будет достигнута максимальная производительность работы оборудования, равная 36 т продукции за смену. Полученную экономию денежных средств в размере 3 ден.ед. можно будет направить на какие-либо иные цели, например, на премирование рабочих, которые будут заниматься отладкой полученного оборудования. На излишнюю площадь в 2 кв.м можно поставить ящик с цветами.
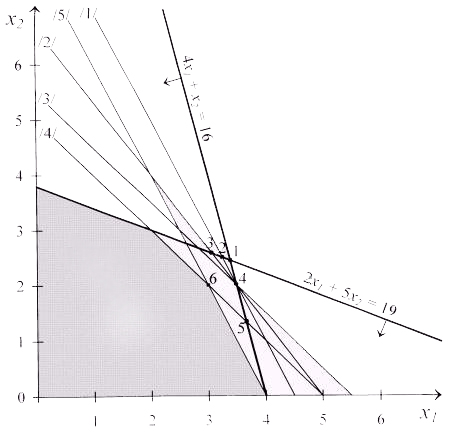
Геометрическая интерпретация метода Гомори: строим множество планов (см. рисунок). В точке 1 - оптимальный нецелочисленный план.
Первое ограничение Гомори: 2/9x3 + 8/9x4 - S1 = 4/9, S1 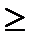 0
0
Из первого ограничения задачи: х3 = 19 - 2х1 - 5х2
Из второго ограничения задачи: х4 = 16 - 4х1 - х2
Подставляем х3 и х4 в первое ограничение Гомори и после преобразований получаем: 4х1 + 2х2 + S1 = 18, S1 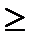 0.
0.
Отсюда имеем: 4х1 + 2х2 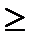 18. Это ограничение отсекает от множества планов область, содержащую точку 1. Новый оптимальный нецелочисленный план - точка 2.
18. Это ограничение отсекает от множества планов область, содержащую точку 1. Новый оптимальный нецелочисленный план - точка 2.
Второе ограничение Гомори: 1/4x3 + 7/8S1 - S2 = 1/2, S2 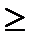 0
0
Из первого ограничения задачи: х3 = 19 - 2х1 - 5х2
Из первого ограничения Гомори: S1 = 18 - 4х1 - 2х2
Получаем: 4х1 + 3х2 + S2 = 20, S2 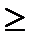 0 или 4х1 + 3х2
0 или 4х1 + 3х2 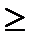 20. Это ограничение отсекает от множества планов область, содержащую точку 2. Новый оптимальный нецелочисленный план - точка 3.
20. Это ограничение отсекает от множества планов область, содержащую точку 2. Новый оптимальный нецелочисленный план - точка 3.
Третье ограничение Гомори: 2/7x3 + 6/7S2 - S3 = 4/7, S3 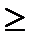 0
0
Из первого ограничения задачи: х3 = 19 - 2х1 - 5х2
Из второго ограничения Гомори: S2 = 20 - 4х1 - 3х2
После подстановки x3 и S2 в третье ограничение Гомори получаем: 4х1 + 4х2 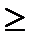 22. Это ограничение отсекает от множества планов область, содержащую точку 3. Новый оптимальный нецелочисленный план - точка 4.
22. Это ограничение отсекает от множества планов область, содержащую точку 3. Новый оптимальный нецелочисленный план - точка 4.
Четвертое ограничение Гомори: 1/4S3 - S4 = 1/2, S4 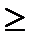 0
0
Из третьего ограничения Гомори: S3 = 22 - 4х1 - 4х2
Получаем: х1 + х2 + S4 = 5, S4 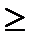 0. Отсюда имеем: х1 + х2
0. Отсюда имеем: х1 + х2 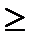 5. Это ограничение отсекает от множества планов область, содержащую точку 4. Новый оптимальный нецелочисленный план - точка 5.
5. Это ограничение отсекает от множества планов область, содержащую точку 4. Новый оптимальный нецелочисленный план - точка 5.
Пятое ограничение Гомори: 1/3x4 + 2/3S4 - S5 = 2/3, S5 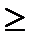 0
0
Из второго ограничения задачи: х4 = 16 - 4х1 - х2
Из четвертого ограничения Гомори: S4 = 5 - х1 - х2
Получаем: 2х1 + х2 + S5 = 8, S5 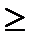 0. Отсюда: 2х1 + х2
0. Отсюда: 2х1 + х2 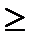 8. Это ограничение отсекает от множества планов область, содержащую точку 5. Оптимальный целочисленный план - точка 6 с координатами (3;2).
8. Это ограничение отсекает от множества планов область, содержащую точку 5. Оптимальный целочисленный план - точка 6 с координатами (3;2).
Заштрихованная часть - целочисленное множество планов.
Поиск по сайту: