Метод сопряженных градиентов

Рассмотренные выше градиентные методы отыскивают точку минимума функции в общем случае лишь за бесконечное число итераций. Метод сопряженных градиентов формирует направления поиска, в большей мере соответствующие геометрии минимизируемой функции. Это существенно увеличивает скорость их сходимости и позволяет, например, минимизировать квадратичную функцию

f(x) = (х, Нх) + (b, х) + а

с симметрической положительно определенной матрицей Н за конечное число шагов п, равное числу переменных функции. Любая гладкая функция в окрестности точки минимума хорошо аппроксимируется квадратичной, поэтому методы сопряженных градиентов успешно применяют для минимизации и неквадратичных функций. В таком случае они перестают быть конечными и становятся итеративными.

По определению, два n -мерных вектора х и у называют сопряженными по отношению к матрице H (или H -сопряженными), если скалярное произведение (x, Ну) = 0. Здесь Н - симметрическая положительно определенная матрица размером п х п.

Одной из наиболее существенных проблем в методах сопряженных градиентов является проблема эффективного построения направлений. Метод Флетчера-Ривса решает эту проблему путем преобразования на каждом шаге антиградиента -f(x [ k ] ) в направление p [ k ], H -сопряженное с ранее найденными направлениями р [0], р [1],..., р [ k -1]. Рассмотрим сначала этот метод применительно к задаче минимизации квадратичной функции.

Направления р [ k ] вычисляют по формулам:

p [ k ] = - f’(x [ k ] ) +b_k-1 p [ k -l], k >= 1;

p [0] = - f ’ (x [0] ).

Величины b _{k -1} выбираются так, чтобы направления p [ k ], р [ k -1] были H -сопряженными:

(p [ k ], Hp [ k- 1]) = 0.

В результате для квадратичной функции

,

итерационный процесс минимизации имеет вид

x [ k +l] =x [ k ] +a_kp [ k ],

где р [ k ] - направление спуска на k- м шаге; а_k - величина шага. Последняя выбирается из условия минимума функции f(х) по а в направлении движения, т. е. в результате решения задачи одномерной минимизации:

.

Для квадратичной функции

Алгоритм метода сопряженных градиентов Флетчера-Ривса состоит в следующем.

1. В точке х [0] вычисляется p [0] = - f’(x [0] ).

2. На k- м шаге по приведенным выше формулам определяются шаг а _k. и точка х [ k+ 1].

3. Вычисляются величины f(x [ k +1] ) и f’(x [ k +1] ).

4. Если f’(x [k+1] ) = 0, то точка х [ k +1] является точкой минимума функции f(х). В противном случае определяется новое направление p [ k +l] из соотношения

и осуществляется переход к следующей итерации. Эта процедура найдет минимум квадратичной функции не более чем за п шагов. При минимизации неквадратичных функций метод Флетчера-Ривса из конечного становится итеративным. В таком случае после (п+ 1)-й итерации процедуры 1-4 циклически повторяются с заменой х [0] на х [ п +1], а вычисления заканчиваются при , где 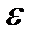- заданное число. При этом применяют следующую модификацию метода:

;

.

Здесь I - множество индексов: I = {0, n, 2 п, Зп,...}, т. е. обновление метода происходит через каждые п шагов.

Геометрический смысл метода сопряженных градиентов состоит в следующем (Рис. 2.11). Из заданной начальной точки х [0] осуществляется спуск в направлении р [0] = -f'(x [0]). В точке х [1] определяется вектор-градиент f'(x [1]). Поскольку х [1] является точкой минимума функции в направлении р [0], то f’(х [1] ) ортогонален вектору р [0]. Затем отыскивается вектор р [1], H -сопряженный к р [0]. Далее отыскивается минимум функции вдоль направления р [1] и т. д.

Рис. 2.11. Траектория спуска в методе сопряженных градиентов

Методы сопряженных направлений являются одними из наиболее эффективных для решения задач минимизации. Однако следует отметить, что они чувствительны к ошибкам, возникающим в процессе счета. При большом числе переменных погрешность может настолько возрасти, что процесс придется повторять даже для квадратичной функции, т. е. процесс для нее не всегда укладывается в п шагов.

Поиск по сайту: