АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Исследование мн-ва клеток транспортной таблицы

Читайте также:
  1. I. Назовите двумембранные органоиды клеток.
  2. I. Сближение и дистантное взаимодействие половых клеток
  3. II. Исследование пульса, его характеристика. Места определения пульса.
  4. II.1.3. Решение транспортной задачи в QSB
  5. III. Статистические таблицы
  6. IIІ Исследование функций
  7. V. Объективное исследование больного.
  8. А. Постановка транспортной задачи.
  9. Автомобильный транспорт в транспортной системе России
  10. Агглютинацией называют склеивание и выпадение в осадок микробных, кровяных или иных клеток под воздействием специфических антител. Впервые описано в 1890 г. M.Charrin и H.Roger.
  11. Адресная миграция клеток
  12. Активный запрос на создание таблицы

Мн-во всех клеток трансп. табл. обозначим U

Опр. Цепью назовем посл-ность клеток, в которой каждые две соседние клетки лежат в одной строке или в одном столбце, но ни в одной строке и ни в одном столбце нет трех послед.клеток.

Опр. Циклом наз. цепь, крайние клетки которой лежат в одной строке или в одном столбце.

Замеч. Если в трансп. табл. соседние клетки соединить отрезками прямых (звеньями цепи), то соседние звенья всегда будут перпендикулярны.

Опр. Мн-во клеток наз. Базисным , полным, если их кол-во равно m+n-1и из его элементов невозможно создать ни одного цикла.

Все остальные клетки наз. небазисными

Опр. План перевозок из i в j 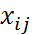наз. базисным, если все перевозки за исключением m+n-1равны 0, а остальные находятся в клетках, составляющих базисные мн-ва клеток.

Опр. Перевозки 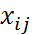, где (i,j) наз. базисными, а если (i,j) 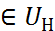, то небазисными.

Опр. Базисный план наз. невырожденным, если все базисные перевозки строго >0, в противном случае – вырожденным.


 


 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)