IIІ Исследование функций

Теорема (третье достаточное условие экстремума и точки перегиба). Пусть функция 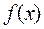имеет в точке производные до п- го порядка включительно, причём 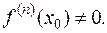Тогда:

1) если 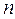– чётное число, то – точка экстремума (точка минимума при и точка максимума при );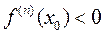

2) если 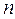– нечётное число, то для графика функции точка 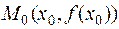является точкой перегиба.

Доказательство. Из условий теоремы следует, что

Эту формулу легко преобразовать к виду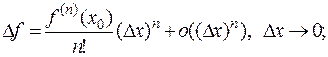

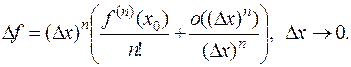
Второе слагаемое в скобках (по смыслу символа 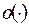) стремится к нулю при 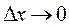, а первое – это некоторое число, отличное от нуля. Поэтому для малых значений знак скобки совпадает со знаком .

Если число 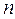– чётное, то и знак не влияет на знак 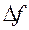, т.е. – точка экстремума. При этом, если то и 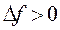, значит – точка минимума, а если то и и – точка максимума.

Если число 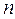– нечётное, то знак 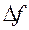зависит от знака . Кроме того, в силу условия 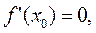касательная к графику функции в точке 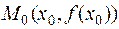– горизонтальная. Следовательно, график слева и справа от этой точки находится по разные сторон от касательной, т.е. в этой точке график имеет перегиб.

Пример 3. Для функции 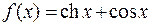точка 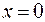является стацио-нарной, ибо 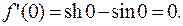Далее:

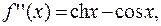
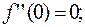
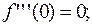
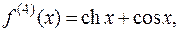
Так как первая, не обратившаяся в ноль производная, чётного порядка, то ноль – точка экстремума, а именно точка минимума, ибо .

Поиск по сайту: