АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

III Формула Тейлора с остаточным членом в форме Лагранжа

Читайте также:
  1. II Формула Тейлора с остаточным членом в форме Пеано
  2. ODBC - открытый интерфейс к базам данных на платформе Microsoft Windows — до 15 мин.
  3. А выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид
  4. Антигенная структура бактерий. Групповые, ввдовые, типовые антигены. Перекрестнореагируюшие антигены. Антигенная формула.
  5. АРХ 6.Представьте в графической форме конструктивные решения плит покрытия размером на пролет: «2Т», «П», КЖС»,. Достоинства и недостатки.
  6. Аудит проведения международных расчетов в форме документарного аккредитива
  7. Аудит расчетов по форме безналичных расчетов
  8. Барометрическая формула
  9. Барометрическая формула. Распределение Больцмана.
  10. Барометрическая формула. Распределение Больцмана.
  11. Барометрическая формула. Распределение Больцмана.

Приведём без доказательства следующую теорему.

Теорема 2. Пусть функция имеет в некотором промежутке, содержащем точку 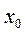, производные до 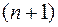-го порядка включительно. Тогда для любого из этого промежутка найдётся точка такая, что

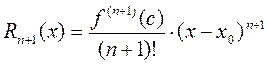
Замечание 1. Форма Лагранжа остаточного члена используется в тех случаях, когда требуется приближённо вычислить при фиксированном значении , отличном от 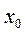. Остаточный член в этой форме напоминает следующий, очередной, член формулы Тейлора, лишь только 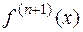вычисляется не в точке 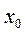, а в некоторой точке 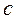между и .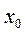

Выпишем формулу Тейлора с учётом теоремы 2:

 

§3. Формула Маклорена. Оценка Rn( x )


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)